 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Speedup
[To Lecture Notes Index]
San Diego State University -- This page last updated February 20, 1996, 1996

Contents of Speedup Lecture
- Parallel Speedup
- References
- How much Speedup is Possible?
- Amdahl's Law - Serial Bottlenecks
- Principle of Unitary Speedup
- Superlinear Speedup in Theory
- Superlinear Speedup in Practice
S. G. Akl, M. Cosnard, and A. G. Ferreira, Data-movement-intensive problems:
two folk theorems in parallel computation revisited, Theoretical Computer
Science 95 (1992) 323-337
G. S. Almasi and A. Gottlieb, Highly Parallel Computing,
Benjamin/Cummings, 1989
comp.parallel newsgroup, January 1995
Cosnard and Trystram, Parallel Algorithms and Architectures,
International Thompson Computer Press, 1995
Definitions
- Ts(N) = time required by best sequential algorithm to solve a problem of
size N
-
- Tp(N) = time required by parallel algorithm using p processors to solve a
problem of size N
-
- Sp(N) = Ts(N)/Tp(N)
-
- Sp(N) is the speedup achieved by the parallel algorithm
Amdahl's law
Assume
- An operation takes one time unit
-
- A fraction 0 < f < 1 of the operations must be done sequentially
Then Sp(N) <= 1/f
Proof:
We have
- f*Ts(N) = number of operations that must be done sequentially
-
- (1-f)*Ts(N) = number of operations that can be done in parallel
We get
- Tp(N) = f*Ts(N) + (1-f)*Ts(N)/p
so
- Sp(N)
- = Ts(N)/(f*Ts(N) + (1-f)*Ts(N)/p)
- = 1/(f + (1-f)/p)
But (1-f)/p < 1
Thus Sp(N) <= 1/f
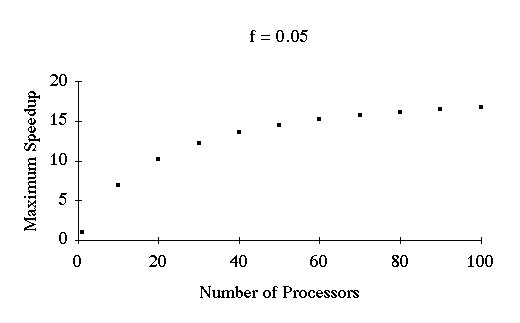
Amdahl's Law with 5% Sequential Operations
Maximum speedup obtainable on an algorithm if 5% of its operations must be done
sequentially
Amdahl's Law Expanded
On many algorithms the fraction of the operations that must be done
sequentially is not a constant f, but a function, f(N), of the size of the
input of the algorithm .
So the law states
- Sp(N) <= 1/f(N)
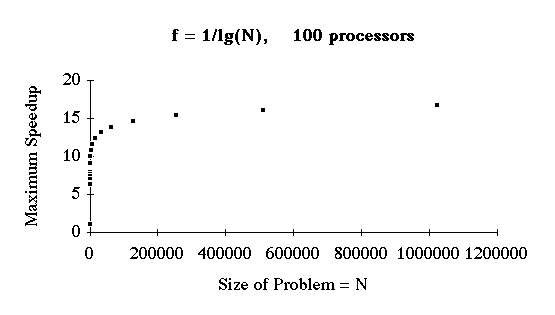
Example - Sorting N Numbers
Assume
- The only operations that must be done sequentially are the reading of the N
numbers from disk
Total amount of work for sorting = [[Theta]]( N*lg(N) )
Sequential operations = [[Theta]]( N )
So
- f(N) = [[Theta]]( N/{N*lg(N)} ) = [[Theta]]( 1/lg(N) )
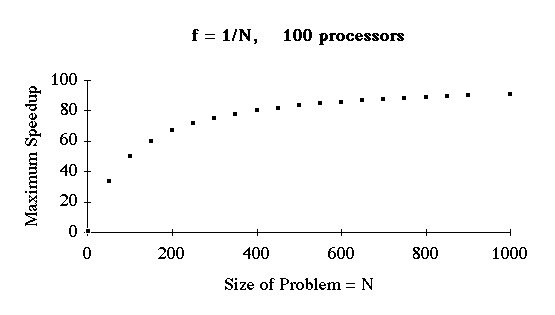
Example Multiplying Two N*N Matrices
Two N*N matrices have a total of 2*N*N elements
Assume
- The only operations that must be done sequentially are the reading of the
2*N*N numbers from disk
The straight forward method of multiplying two matrices takes
[[Theta]]( N*N*N ) operations
Sequential operations = [[Theta]]( N*N )
So
- f(N) = [[Theta]]( N*N/{N*N*N} ) = [[Theta]]( 1/N )
How realistic are these two examples?
Lee's Generalized Amdahl's Law
Let qk be the percentage of the program that can be executed with k
processors.
Let t1 be the time to run the program sequentially.
We have:
-
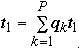 and
and
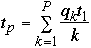
So
-
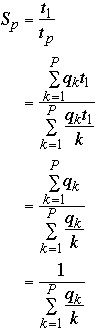
Setting qk = 1/p w get
-
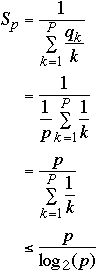
So
-
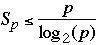
Stone's table (1973)
| Speed Up | Examples |
| a*p | Matrix computations |
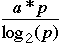 | Sorts, Linear recursions, polynomial evaluation |
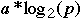 | Search for an element in a set |
Lemma 1:
- If N processors can perform a computation in one step, then P processors
can perform the same computation in ceiling(N/P) steps for 1 <= P <=
N
proof:
- Each of the N original processors performs one operation
-
- Call that operation I[j ] for j = 1, ..., N
-
- Each of the P processors performs the operation of ceiling(N/P) original
processors
-
- So each of the P processors must perform ceiling(N/P) operations
-
- Note the P'th processor may perform fewer operations
Corollary:
- If P processors can perform a computation in one step, then one processors
can perform the same computation in P steps
Folk Theorem 1. Unitary Speedup
- For any algorithm of size N and any number of processors P we have Sp(N)
<= P. That is Ep(N) <= 1
proof:
- Ts(N) = time required by best sequential algorithm to solve a problem of
size N
-
- Tp(N) = time required by parallel algorithm using p processors to solve a
problem of size N
-
- Sp(N) = Ts(N)/Tp(N)
-
- Using the corollary a single processor can perform the same operations as
the P processors in P*Tp(N) time
-
- So Ts(N) <= P*Tp(N)
-
- Thus Sp(N) <= P*Tp(N) / Tp(N) = P
Folk Theorem 2. (Brent)
- If an algorithm involving a total of N operations can be performed in time
T on a PRAM with sufficiently many processors, then it can be performed in time
T + (N - T)/P on a PRAM with P processors.
proof:
- Let Si be the operations performed at time step i on all of the original
processors, i = 1, ..., T
-
-
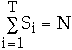
-
- Using P processors, the i'th step can be simulated in ceiling(Si /P) time
-
- But ceiling(Si /P) <= (Si /P) + (P - 1)/P
-
-
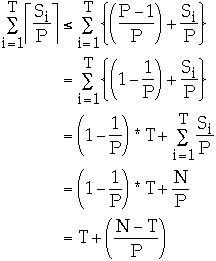
Uses of Brent's Theorem
- Simplify analysis
- Justify algorithms with large number of processors
- Produce optimal parallel algorithms
- It is possible to improve a parallel algorithm by using few
processors
Example - Parallel Add
Adding N integers with P = N/2 processors
Assume that N is a power of 2
J = N/2
while J >= 1 do
for K = 1 to J do in Parallel
Processor K: A[K] = A[2K-1]+A[2K]
end for
J = J/2
end while
Time Complexity [[Theta]]( lg(N) )
Cost [[Theta]]( N*Lg(N) )
Optimal Parallel Add
Let P = ceiling( N/lg(N) ) be the number of processors
for I = 1 to P do in Parallel
Processor I:
B[I] = 0;
for K = 1 to lg(N) do
B[I] = A[{(I-1)*N/P}+K] + B[I]
end for
end for
J = ceiling(N/[2*lg(N)])
while J >= 1 do
for K = 1 to J do in Parallel
Processor K: B[K] = B[2K-1]+B[2K]
end for
J = J/2
end while
Time Complexity [[Theta]](lg(N)) + [[Theta]]( lg[N/lg(N)] )= [[Theta]]( lg(N)
)
Cost [[Theta]]( Lg(N) * N/lg(N) ) = [[Theta]]( N )
Problem: Messy List
- We are given P distinct integers I1, I2, ..., IP such that Ik <= P for
all k.
-
- Note Ik can be negative.
-
- The integers are stored in an array A, such that A[K] = Ik
-
- Modify A so that for 1 <= K <= P we have:
- A[Ik] = Ik if and only if 1 <= Ik <= P
-
- A[K] = Ik otherwise
Example
Let P = 4
A[1] A[2] A[3] A[4]
Original values 4 1 -2 3
Modified values 1 1 3 4
Parallel Solution
for I = 1 to P do in Parallel
Processor I: A[A[I]] := A[I]
Time required: 1 time unit
Sequential Solution
Theorem.
- The problem Messy List cannot be solved in less than 2P -1 time units using
the RAM model.
proof:
At some point the solution will perform an operation like:
- Read X; if X > 0 then A[X] = X
- (1)
-
- Consider the first time we perform such an operation
-
- Since we overwrite A[X] in line (1) we need to save old value of A[X]
before we do line (1)
-
- But X can be any index between 1 and P so we need to save P -1 elements of
A before we perform (1)
-
- We also need to perform (1) P times.
The speedup is 2P -1
Superlinear speedups are found in practice
All examples that I know of are due to the additional resources used in the
parallel code over that used in the sequential code
Cache effects are a common cause of superlinear speedups
The following example is from comp.parallel Jan. 1995
Newsgroups: comp.parallel
Subject: Help - explain superlinear speedup?
From: slater@nuc.berkeley.edu (Steve Slater)
- I have a program which has superlinear speedup and I can't explain it. Does
anyone have any ideas. Here is the summary.
-
- I am using a code which passes messages using p4, on 4 Sparc 2's running
SunOS 4.1.3. The code solves coupled matrix equations, much like a heat
equation. The processors are each assigned a geometrical region like:
------------------
| | |
| A | B |
|________|_______|
| | |
| C | D |
|________|_______|
- Each job/process analyzes only one region of A through D.
-
- What happens in the code (not really important to my problem though) is a
matrix is solved for each A-D, then the boundary conditions are passed between
each region (outgoing heat current = incoming for each neighbor) and the matrix
equations are solved locally again. The process repeats until the solution
converges.
-
- With p4, I first run 4 processes (4 regions) on only 1 machine. The
messages are passing through sockets. Then I run on 2 machines, each having 2
processes (2 regions), and finally on 4 machines, each having 1 process
(region).
-
- You would expect less than linear speedup since with only one machine, no
messages are sent over the ethernet, they are just communicated via sockets.
But I get very superlinear speedup like:
-
- 1 proc:556 sec 4 unique processes on 1 machine
- 2 proc:204 sec 2 processes on each of 2 machines
- 4 proc: 38 sec 1 process on each machine
-
- There was NO memory swapping occurring during the entire execution time. I
would periodically check with ps.
-
- Does anyone have any thoughts?
Steve Slater
slater@nuc.berkeley.edu
From: Krste Asanovic <krste@icsi.berkeley.edu>
Subject: Re: Help - explain superlinear speedup?
- There are two possible cache effects. The first is that each Sparc-2 only
has 64KB of unified cache. If your data set + code fits into 64KB you'll see a
marking improvement over the case when it doesn't.
-
- The second is the limited TLB size. I don't have the Sparc-2 MMU numbers
handy, but I think it supported 64 entries for 4KB pages, i.e. 256KB mapped
simultaneously at most. If a single process's code + data fits into the TLB,
you'll see a marked difference.
-
- These differences are exaggerated if your code makes repeated sweeps over
these data regions.
--
Krste Asanovic email: krste@icsi.berkeley.edu
Newsgroups: comp.parallel
From: David Bader <dbader@glue.umd.edu>
Subject: Re: Help - explain superlinear speedup?
- Superlinear speedup is commonly attributable to caching effects. When you
split the problem onto multiple processors, the subproblems are obviously a
fraction of the original problem size. With the smaller problem size, you are
most likely getting a higher cache hit rate, and the result, even after
considering the communications time, is still better than the time on a single
processor with more cache misses.
-david
Newsgroups: comp.parallel
From: mtaylor@easynet.com (Michael A. Taylor)
Subject: Re: Help - explain superlinear speedup?
- You are reducing the number of process switches and also the cache flushing
that occurs with each process switch. Therefore you are executing fewer
instructions (less switches) and they execute faster (fewer cache
faults).


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms