 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Numerical Methods part 2
[To Lecture Notes Index]
San Diego State University -- This page last updated April 30, 1996

Contents of Numerical Methods part 2 Lecture
- Linear Equations
Matrix Matrix Multiplication and Scan
Let A and B be a n*n matrices
Compute C = A*B
-
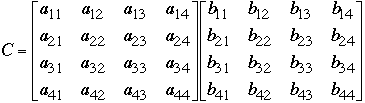
We have
-
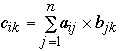
Scan can compute
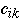 in log(n) time using n/2 processors
in log(n) time using n/2 processors
Since there are
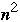 elements of C
elements of C
Scan takes log(n) time with
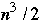 processors to compute C
processors to compute C
Slowdown
Let A, B, and C be a n*n matrices such that
- C = A*B
Let
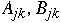 be (n/2)*(n/2) matrices such that
be (n/2)*(n/2) matrices such that
-
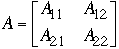 and
and
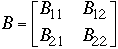
Then
-
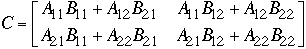
Strassen's Method
Let A, B, and C be a 2*2 matrices such that
- C = A*B
-
-
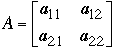 ,
,
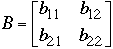 ,
and
,
and
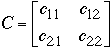
Define the sums and products:
Then we have:
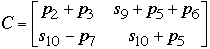
Using 7 multiplications and 15 additions
On n*n matrices the above method take O(
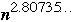 )
operations
)
operations
Solving a system of linear equations like:
-
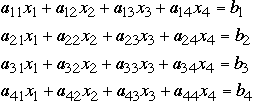
can be reduced to solving Ax = b for x where:
-
-

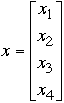
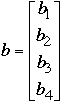
Gauss-Jordan Method
for j = 1 to n do
for h = 1 to n do
for k = j to n + 1 do
if (h != j) then 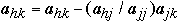 end for
end for
end for
for j = 1 to n do
end for
end for
end for
for j = 1 to n do
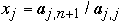 end for
end for
Gauss-Jordan Method - SIMD
for j = 1 to n do
for h = 1 to n do in parallel
for k = j to n + 1 do in parallel
if (h != j) then 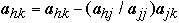 end for
end for
end for
for j = 1 to n do in parallel
end for
end for
end for
for j = 1 to n do in parallel
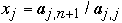 end for
end for
T(n) = O(n)
P(n) = O(
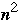 )
)
Another Approach
If Ax = b then x =
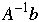
So just compute
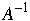
Special Case
Let
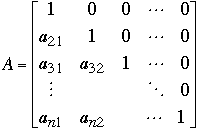
Define
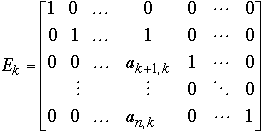
We have:
- 1)
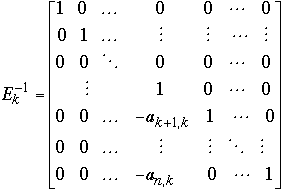
-
- 2)
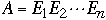
-
- 3) if A = BC then
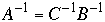
-
- 4)
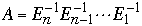
So how long does it take to compute
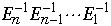 ?
?
Note that A(BC) = (AB)C when A, B, C are n*n matrices
So we can use generalized scan operator with matrix multiplication
Sequential matrix multiplication takes
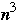
So with n processors we can compute
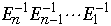 in
in
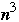 log(n)
time
log(n)
time
But using a scan within a scan to perform all matrix multiplications we can
compute
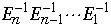 in
in
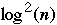 time using
time using
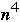 processors
processors
Theorem. L. Csanky 1976
- The A be a nonsingular n*n matrix. Then
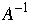 can be computed in parallel using
can be computed in parallel using
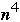 processors in
processors in
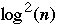 time.
time.
proof.
- Uses some cool math to do some fancy stuff
-
- Details available on demand
-
- Method is not practical due to number of processors required and numerical
problems
It is an open problem if
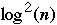 time is best possible for computing inverse of an n*n matrix
time is best possible for computing inverse of an n*n matrix
It is an open problem if
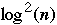 time is best possible for triangular matrices
time is best possible for triangular matrices
x =
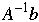 General Case
General Case
Let
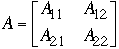 where
where
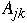 are n/2*n/2 matrices
are n/2*n/2 matrices
We get:
-
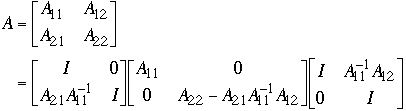
So
-
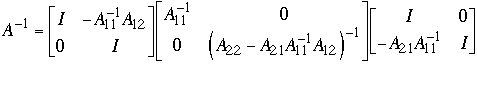
Compute
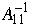 and
and
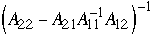 recursively
recursively
This requires O(
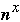 )
sequential time, where 2 < x < 2.5
)
sequential time, where 2 < x < 2.5


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithmsend for end for end for for j = 1 to n do
end for
end for end for end for for j = 1 to n do in parallel
end for