 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Numerical Methods 1
[To Lecture Notes Index]
San Diego State University -- This page last updated April 25, 1996

Contents of Numerical Methods 1 Lecture
- Numerical Algorithms
- Matrix Algorithms
- Transposition
- Matrix Multiplication
Basic Issue - Digital computers don't do math (like math books)
-
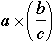 may not the same as
may not the same as
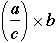
-
-
-
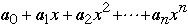 may not be the same as
may not be the same as
-
-
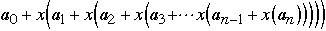
Problem 1. Errors
Let c = a =
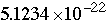 and let b=
and let b=
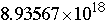
What is
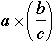 ?
?
What is
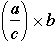 ?
?
Problem 2. Computational Complexity
Computing
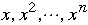 requires n multiplications
requires n multiplications
So computing
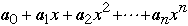 requires
requires
- 2n multiplications and n additions
But
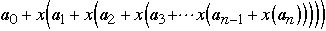 requires
requires
- n multiplications and n additions
Compute
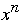 Method 1
Method 1
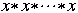
Requires n multiplications
Method 2
Let
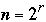
Algorithm
- Result = x
- for k = 1 to r do
- Result = Result * Result
Requires log(n) multiplications
Let n be any value
Let
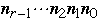 be the binary representation of n
be the binary representation of n
Then
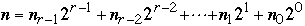
So
-
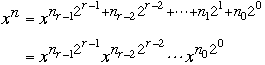
but in log(n) multiplications we can compute all the terms
-
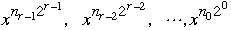
It takes another log(n) multiplications to multiply them together
Problem 3
It can take more human effort and some deep mathematics to perform numerical
analysis
Let A be an n*n matrix, for example
-

The transpose,
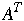 ,
of A is obtained by mapping
,
of A is obtained by mapping
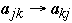 for all j and k
for all j and k
-
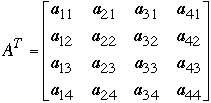
Computing
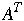 from A sequentially by:
from A sequentially by:
for j = 2 to n do
for k = 1 to j - 1 do
temp = A[ j, k ]
A[ j, k ] = A[ k, j ]
A[ k, j ] = temp
end for
end for
Time Complexity = O(n*n)
EREW Transpose
Use (n*n - n)/2 processors
for j = 2 to n do in parallel
for k = 1 to j - 1 do in parallel
Processor P(j, k)
temp = A[ j, k ]
A[ j, k ] = A[ k, j ]
A[ k, j ] = temp
end for
end for
Time Complexity = O( 1 )
Cost = n*n
Big Deal!What about Networks?
Transpose on Shuffle-Exchange
Let n =
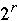 and use shuffle-exchange network with
and use shuffle-exchange network with
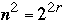 processors
processors
Map elements of A to the processors by:
-
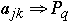 where
where
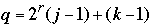 for j, k = 1 to n
for j, k = 1 to n
Note:
- (j-1) and (k-1) range from 0 to n-1
-
- (j-1) and (k-1) take r bits to store
So
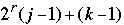 can be obtained by writing the bits of ( j - 1) then following them with the
bits of (k-1).
can be obtained by writing the bits of ( j - 1) then following them with the
bits of (k-1).
Algorithm
Shuffle r times
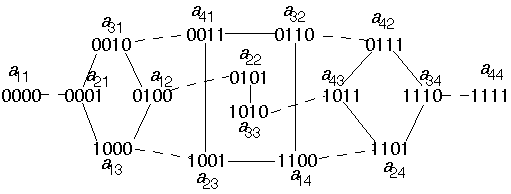
Example 1
Let r = 1 so n = 2
We have
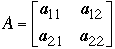 and
and
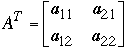
Map to the 4 node shuffle-exchange network
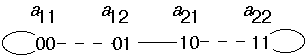
Now perform 1 shuffle on all nodes
Example 2
Let r = 2 so n = 4
We have
 ,
,
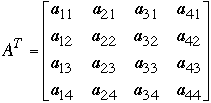
map to the 16 node shuffle exchange network

now perform 2 shuffles
Let A be an n*n matrix, and x be a vector with n elements
Compute y = Ax
-
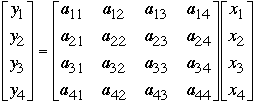
We have
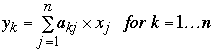
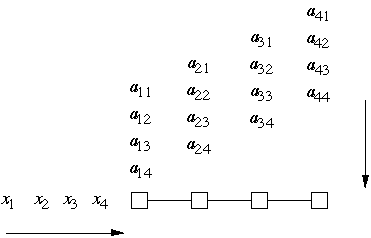
Matrix-Vector Multiplication on Linear Array
Matrix Matrix Multiplication
Let A and B be a n*n matrices
Compute C = A*B
-
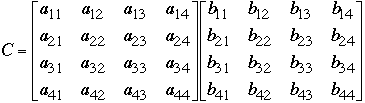
We have
-
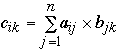
This requires n multiplications and n-1 additions per element of C
So it takes
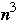 multiplications and
multiplications and
 additions to compute C
additions to compute C
Matrix-Matrix Multiplication on Linear Array
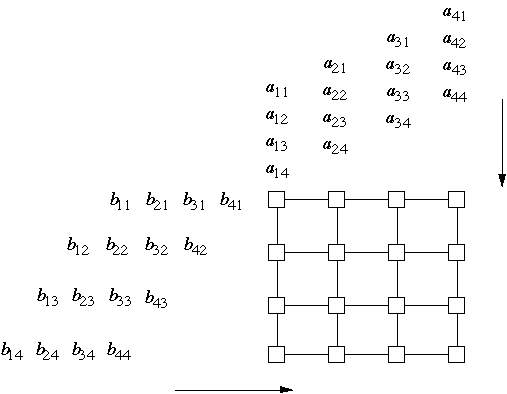


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms