 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Batcher's Sort
[To Lecture Notes Index]
San Diego State University -- This page last updated February 29, 1996, 1996

Contents of Batcher's Sort Lecture
- Parallel Sorting
- Batcher's Odd-Even Sorting Circuit
- Complexity Of Odd-Even Merging
- Sorting By Merging
Let A and B be sorted lists of length n, n is even
Let OM be the sorted list of length n formed by sorting the elements in the odd
positions (1, 3, 5, ...) of A and B
Let EM be the sorted list of length n formed by sorting the elements in the
even positions (2, 4, 6, ...) of A and B
Let R be the sorted list of size 2n formed by merging A and B.
Let AJ, BJ, OMJ, EMJ, RJ be the J'th element of the corresponding lists A, B,
OM, EM, R.
Example
A 1 2 3 15 20 21
B 6 7 8 9 10 30
OM 1 3 6 8 10 20
EM 2 7 9 15 21 30
R 1 2 3 6 7 8 9 10 15 20 21 30
Lemma.
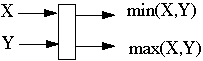
R1 = OM1, R2n = EMn
R2k = min(OMk+1, EMk)
R2k+1 = max(OMk+1, EMk)
Comparator Circuit
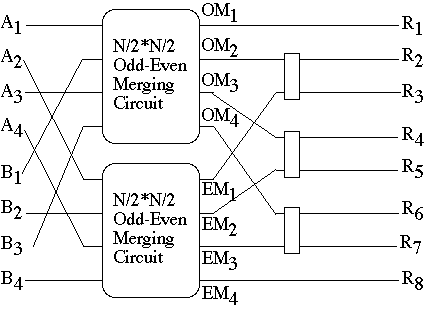
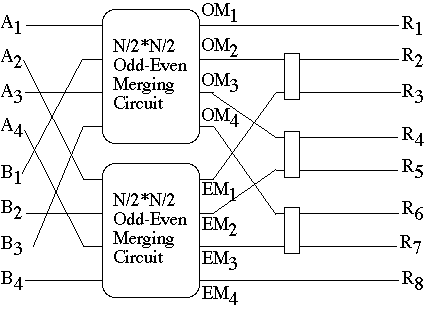
N*N Odd-Even Merging CircuitRecursive Definition (N = 4)
1*1 Odd-Even Merging Circuit
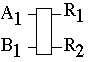 2*2 Odd-Even Merging Circuit
2*2 Odd-Even Merging Circuit
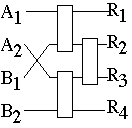 4*4 Odd-Even Merging Circuit
4*4 Odd-Even Merging Circuit
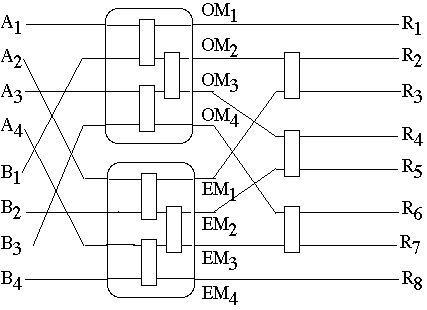
8*8 Odd-Even Merging Circuit
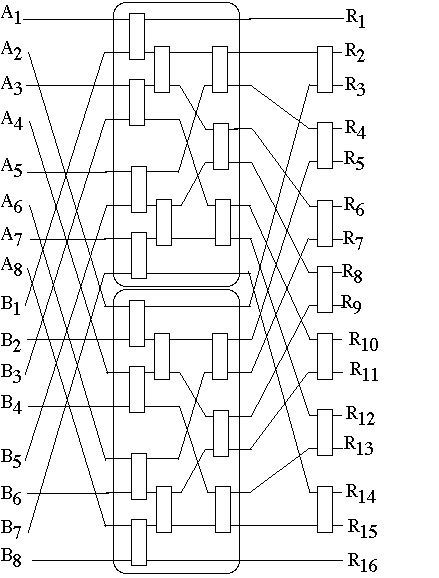
Let T(2N) = time required to merge two sorted lists of size N each
Then T(2) = 1 and T(2N) = T(N) + 1
So T(2N) = 1 + lg(N)
Let CC(2N) = the number of comparator circuits needed to merge two sorted lists
of size N each
Then CC(2) = 1 and CC(2N) = 2*CC(N) + (N-1)
So CC(2N) = 1 + N*lg(N)
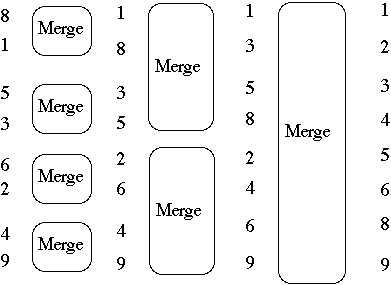
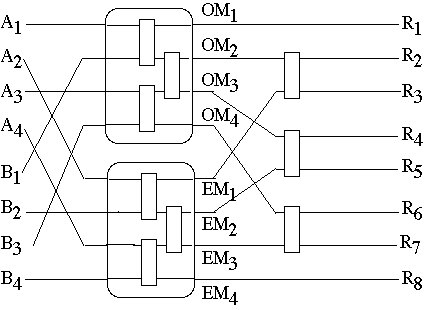
Sorting N = 2K items requires K = lg(N) merge passes
- N = 8
- Pass 1 needs 4 (1*1) merge circuits
- time 1
- Pass 2 needs 2 (2*2) merge circuits
- time 1 + lg(2) = 2
- Pass 3 needs 1 (4*4) merge circuits
- time 1 + lg(4) = 3
Pass L needs N/2L (2L-1*2L-1) merge circuits
time 1 + lg(2L-1) = L
T(N) = time required to sort list of size N = 2K
-
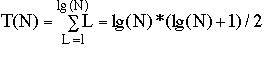
Number of Comparator Circuits in Batcher's Odd-Even Sort
Sorting N = 2K items requires K = lg(N) merge passes
Pass L needs N/2L (2L-1*2L-1) merge
circuits
(2L-1*2L-1) merge circuit uses 1 +
2L-1*lg(2L-1) = 1 + (L-1)*2L-1 comparator
circuits
CC(N) = the number of comparator circuits needed in Batcher's Odd-Even Sort to
sort a list of N = 2K items
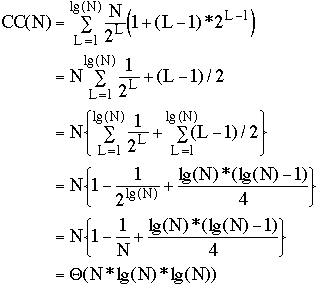
Number of Processors in PRAM needed for
Batcher's Odd-Even Sort
P(N) = N/2
T(N) = lg(N)*(lg(N) + 1)/2
C(N) = N*lg(N)*(lg(N) + 1)/4
SN/2(N) = Ts(N)/Tp(N) = 2N/(lg(N) + 1)
Batcher's Odd-Even Sort on PRAM
Batcher's Merge-Exchange Sort
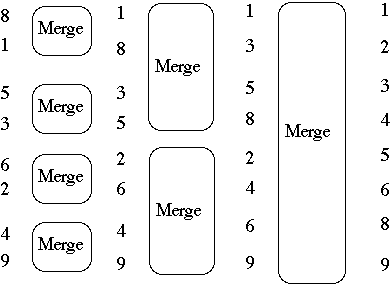
8 merge 6 regroup 6 merge 4 merge 1
1 1 1 1 2
5 4 4 5 3
3 3 3 2 4
6 8 8 6 5
2 2 2 3 6
4 5 5 8 8
9 9 9 9 9
Why?
Straighten out some wiresMakes the indexing easier
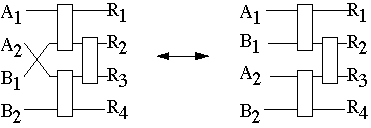
Batcher's Merge-Exchange Sort
Input: N and array A[1:N] of items to sort
set
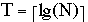
for P = 2T-1, 2T-2, 2T-3, ..., 1 do
- R = 0, D = P
-
- for Q = 2T-1, 2T-2, 2T-3, ..., P do
- for (K = 1 to N - D ) and ((K-1)
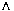 P) = R do in parallel
P) = R do in parallel
-
- if A[K] > A[K + D] then
-
- swap(A[K], A[K + D ])
- end if
- end for
-
- D = Q - P
- R = P
- end for
end for
(K + 1)
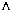 P means logical and of K and P
P means logical and of K and P
If number of processors is less than N than the swap becomes a merge


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms