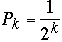CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
Fall Semester, 1996
Splay Performance
[To Lecture Notes Index]
San Diego State University -- This page last updated Nov 14, 1996

Contents of Splay Performance
- Zipf's Law
Zipf noticed that in English the frequency of word usage follows:
-
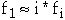
where fi denotes the frequency of the ith most frequent
word
Zipfian Probability Distribution:
Assume we have a list of n items:
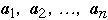
The a's are ordered by frequency of access
Probability of accessing item
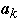 is
is
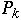 and
and
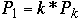
Then
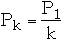
But
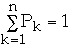 so we have
so we have
-
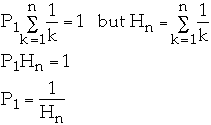
Zipfian Probability Distribution
Let
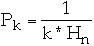 for k = 1, 2, ..., n
for k = 1, 2, ..., n
where
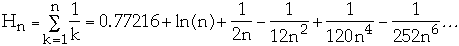
Pk
n
= 2
n = 3
| k | 1 | 2 | 3 |
| Pk | 0.5455 | 0.2727 | 0.1818 |
n = 4
n = 5
| k | 1 | 2 | 3 | 4 | 5 |
| Pk | 0.438 | 0.219 | 0.146 | 0.109 | 0.0876 |
n = 6
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| Pk | 0.408 | 0.204 | 0.136 | 0.102 | 0.0816 | .0680 |
How to Implement Zipf's Distribution
Let
-
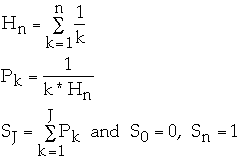
Method 1
If
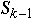 <= rand() <
<= rand() <
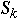 then return k
then return k
Method 2
For sample of size N
- let item a1 be included N * P1 times
- let item a2 be included N * P2 times
Exp (?) Distribution
let
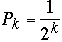
Move-to-root vs. Splay Training
Insert integers 1 - Tree Size in random order
Same random order used to build each tree
Create a Zipfian sample of size "Sample"
Access each sample item in a tree
Each tree gets different sample
| Tree Size 800 | | Tree Size 1600 | |
| Sample 100 | | Sample 200 | |
| Splay | MtoR | Splay | MtoR |
| 31 | 18 | 50 | 49 |
| 18 | 41 | 37 | 42 |
| 18 | 17 | 42 | 40 |
| 18 | 19 | 38 | 40 |
| 18 | 18 | 38 | 42 |
| 20 | 18 | 38 | 38 |
| 17 | 17 | 36 | 38 |
| 17 | 17 | 37 | 38 |
| 18 | 17 | 38 | 35 |
| 19 | 15 | 36 | 37 |
| 16 | 17 | 35 | 36 |
| 17 | 14 | 37 | 37 |
| 17 | 17 | 37 | 33 |
| 18 | 16 | 36 | 35 |
| 16 | 15 | 35 | 34 |
| 16 | 16 | 37 | 35 |
| 27 | 16 | 35 | 35 |
| 16 | 16 | 38 | 37 |
| 15 | 16 | 37 | 37 |
| 18 | 15 | 37 | 35 |
Building Trees
Integers from 1 to N are inserted into a tree in random order
Each tree is created with the same random sequence
Times are in milliseconds
| Size | BST | AVL | Splay | MoveToRoot |
| 200 | 17 | 23 | 45 | 52 |
| 400 | 25 | 34 | 97 | 97 |
| 800 | 55 | 69 | 222 | 222 |
| 1600 | 116 | 146 | 499 | 490 |
| 3200 | 246 | 305 | 1136 | 1092 |
| 6400 | 531 | 650 | 2446 | 2406 |
| 12800 | 1155 | 1340 | 5330 | 5196 |
| 25600 | 2617 | 2835 | 11519 | 11246 |
Accessing Nodes in a Tree
In a tree of size N, accessed N keys
Keys to access were selected according to a distribution of keys in tree
Keys access were in random order
In each tree used the same keys in the same order
Exp Distribution
| Size | BST | AVL | Splay | MoveToRoot |
| 200 | 9 | 5 | 9 | 8 |
| 400 | 22 | 11 | 18 | 16 |
| 800 | 30 | 25 | 35 | 32 |
| 1600 | 64 | 55 | 68 | 61 |
| 3200 | 168 | 122 | 135 | 122 |
| 6400 | 422 | 264 | 260 | 254 |
| 12800 | 707 | 489 | 512 | 467 |
| 25600 | 1555 | 1240 | 1029 | 979 |
Zipf Distribution
| Size | BST | AVL | Splay | MoveToRoot |
| 200 | 7 | 5 | 28 | 28 |
| 400 | 14 | 12 | 69 | 64 |
| 800 | 30 | 24 | 148 | 140 |
| 1600 | 69 | 60 | 326 | 318 |
| 3200 | 141 | 120 | 697 | 682 |
| 6400 | 344 | 265 | 1521 | 1482 |
| 12800 | 713 | 618 | 3341 | 3213 |
| 25600 | 1676 | 1251 | 7197 | 6972 |
 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms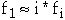
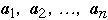
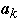 is
is
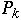 and
and
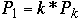
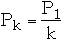
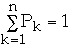 so we have
so we have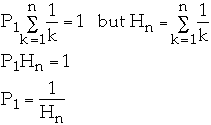
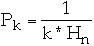 for k = 1, 2, ..., n
for k = 1, 2, ..., n 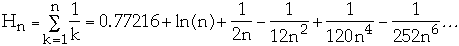
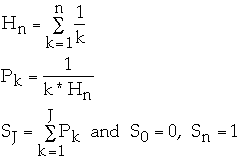
 <= rand() <
<= rand() <
 then return k
then return k