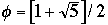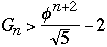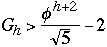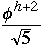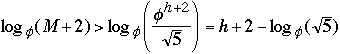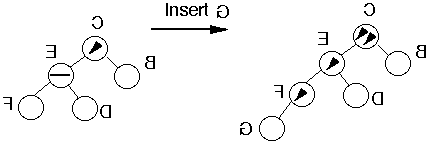CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
Fall Semester, 1996
AVL Trees
[To Lecture Notes Index]
San Diego State University -- This page last updated Oct 17, 1996

Contents of AVL Trees
- References
- Height-Balanced Trees
- AVL Trees
- Insertion into a AVL Tree
- Deletions from an AVL Tree
- Performance of AVL Trees
Data Structure Techniques, Standish, 1980, section 3.7.3
Handbook of Algorithms and Data Structures, Gonnet, 1984, section
3.4.1
Height of a tree is the length of the longest path from the root to a leaf.
A binary search tree T is a height-balanced k-tree or HB[k]-tree, if each node
in the tree has the HB[k] property
A node has the HB[k] property if the height of the left and right subtrees of
the node differ in height by at most k.
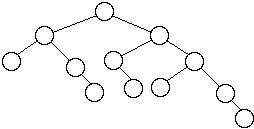
Some HB[2] Trees
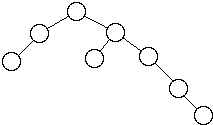
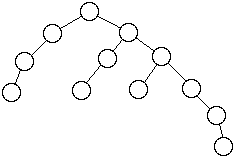
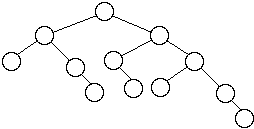
A HB[1] tree is called an AVL tree.
Adel'son-Vel'skii and Landis first defined HB[1] trees
 Worst Case AVL Trees
Worst Case AVL Trees
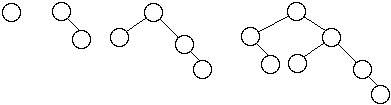
Let
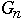 = the number of nodes in worst case AVL tree of height n
= the number of nodes in worst case AVL tree of height n
We have:
-
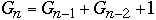
Fibonacci Numbers
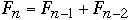 ,
,
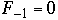 ,
,
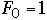
| n | 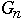 | 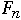 |
| 0 | 1 | 1 |
| 1 | 2 | 1 |
| 2 | 4 | 2 |
| 3 | 7 | 3 |
| 4 | 12 | 5 |
| 5 | 20 | 8 |
| 6 | 33 | 13 |
We get
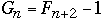
But
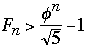 where
where
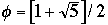
So
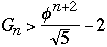
Now take any AVL tree of height h with M nodes, we have
M >=
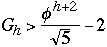
So M + 2 >
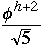
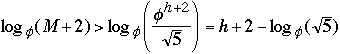
h < 1..4404 lg(M + 2) - 0.328
Theorem ( Adel'son-Vel'skii and Landis 1962) The height of a balanced
tree with N internal nodes always lies between lg (N +1 ) and 1..4404 lg(M + 2)
- 0.328
Some notationBalance Information
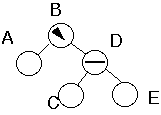
Height of Subtrees
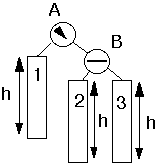
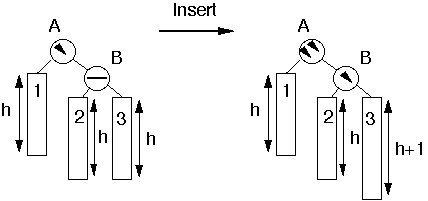
Insert key as normal binary search tree
Restructure the tree if some node are unbalanced
Case 0Inserting into Short Subtree
Balance Information ChangesNo Restructure of Tree
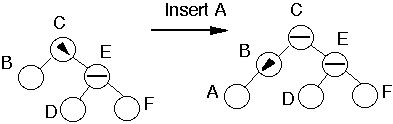 General Case
General Case
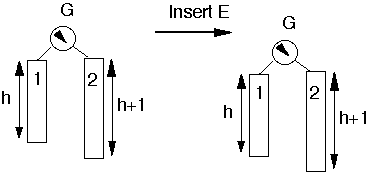 or
or
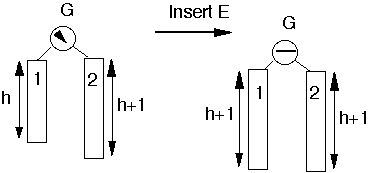
Case 1a
Insert into taller subtreeTaller subtree balancedTaller subtree on RightInsert into outer subsubtree
Example
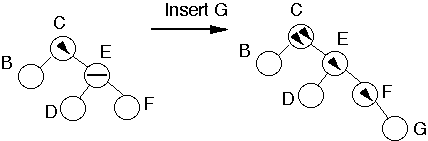 Perform Single Rotation
Perform Single Rotation
Tree is balanced
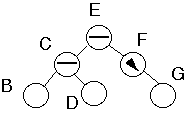
Need for Generalized Case 1a
Case 1a
Insert into taller SubtreeTaller Subtree balancedTaller subtree on RightInsert into outer subsubtree
Add node to subtree 3
 Perform Single Rotation
Perform Single Rotation
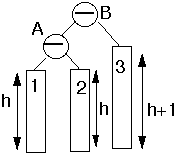
Tree is balanced
Case 1b
Insert into taller subtreeTaller subtree balancedTaller subtree on LeftInsert into outer subsubtree
This is symmetric to case 1a
Example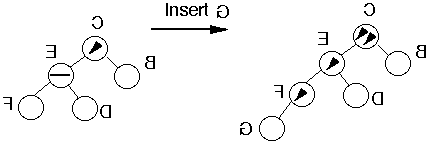
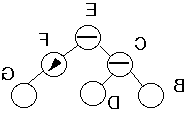
Case 2a
Insert into taller subtreeTaller subtree balancedTaller subtree on RightInsert into inner subsubtree
 Double Rotation
Double Rotation
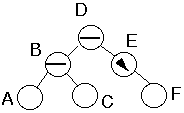
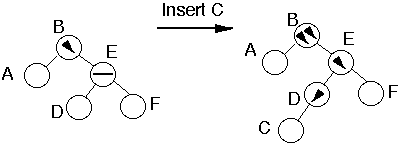
Case 2a
Insert into taller subtreeTaller subtree balancedTaller subtree on RightInsert into inner subsubtree
Insert into subtree 2 or 3
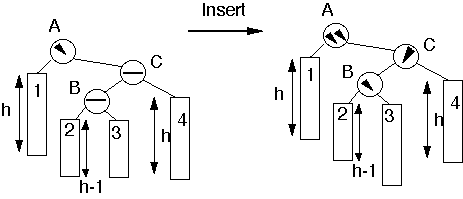
Double Rotation
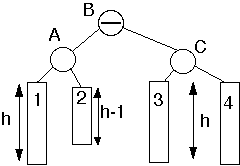
Case 2b
Insert into taller subtreeTaller subtree balancedTaller subtree on LeftInsert into inner subsubtree
This is symmetric to case 2a
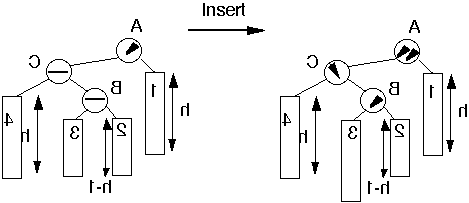
Case 3a
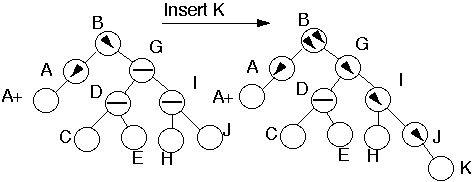
Insert into taller subtreeTaller subtree unbalancedTaller subtree on RightTaller subsubtree on RightInsert into outer subsubsubtree
Insert K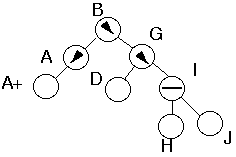 Reduces to Case 1aInsert K
Reduces to Case 1aInsert K
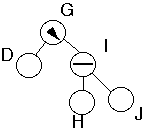
We have covered all cases!
Delete the node as in a binary search tree
The node deleted will be either a leaf or have just one subtree
Since this is an AVL tree if the deleted node has one subtree, then that
subtree contains only one node
Traverse up the tree from the deleted node checking the balance of each node
Case 1a
Traversing Up from Left subtreeDeletion reduced the height of the left subtreeNode has equal balance
Action:
- Change balance of the node and stop
- Have not effected the balance of any higher nodes
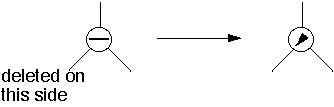 Case 1b
Traversing Up from Right subtreeDeletion reduced the height of the Right subtreeNode has equal balance
Case 1b
Traversing Up from Right subtreeDeletion reduced the height of the Right subtreeNode has equal balance
Action:
- Same as 1a
Case 2a
Traversing Up from Left subtreeDeletion reduced the height of the left subtreeLeft subtree was greater then the right subtree
Action:
- Change balance of the node and stop
- May have effected the balance of any higher nodes, so continue up
tree
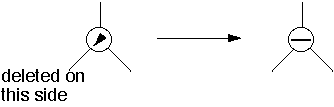
Case 2b
Traversing Up from Right subtreeDeletion reduced the height of the Right subtreeRight subtree was greater then the Left subtree
Action:
- Similar to 2a
Case 3a
Traversing Up from Left subtreeDeletion reduced the height of the left subtreeRight subtree was greater then the Left subtree Left subtrees has equal subsubtrees
Action:
- Perform single rotation, Adjust the balance
- Have not effected the balance of any higher nodes
- Stop here
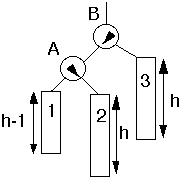
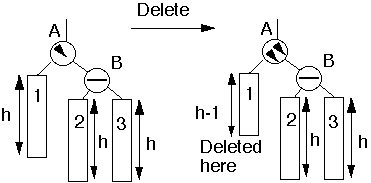 Single Rotation
Single Rotation
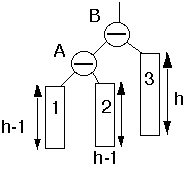
Case 4a
Traversing Up from Left subtreeDeletion reduced the height of the left subtreeRight subtree was greater then the Left subtree One or both of B subtrees has height h-1
Action:
- Double rotation at B
- May have effected the balance of any higher nodes, so continue up
tree
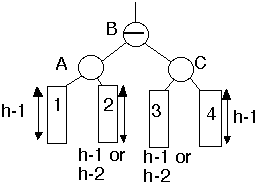
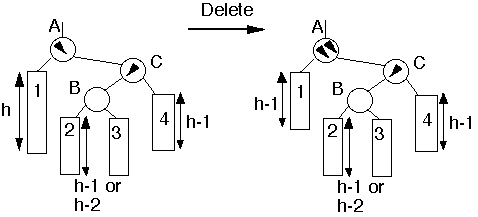 Double Rotation
Double Rotation
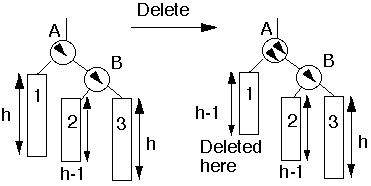
Case 5a
See picture
Action:
- Single rotation at B
- May have effected the balance of any higher nodes, so continue up
tree
Theorem. An insertion into an AVL tree requires at most one rotation to
rebalance a tree. A deletion may require lg(N) rotations to rebalance the
tree.
Simulation Results AVL
| n | C(n) | E[ h(n) ] | R(n) |
| 5 | 2.2 | 3.0 | 0.213 |
| 10 | 2.907 | 4.0 | 0.318 |
| 50 | 4.930 | 6.947 | 0.427 |
| 100 | 5.889 | 7.999 | 0.444 |
| 500 | 8.192 | 10.923 | 0.461 |
| 1000 | 9.202 | 11.998 | 0.463 |
| 5000 | 11.555 | 14.936 | 0.465 |
| 10000 | 12.568 | 15.996 | 0.465 |
n
= number of nodes in the tree
C(n) = average number of comparisons to find a key
E[ h(n) ] = expected height of tree
R(n) = average number of rotations per insertion/deletion
 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms






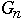 = the number of nodes in worst case AVL tree of height n
= the number of nodes in worst case AVL tree of height n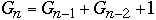
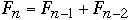 ,
,
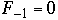 ,
,
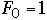
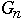
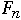
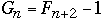
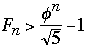 where
where