 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
Fall Semester, 1996
Network Flow
[To Lecture Notes Index]
San Diego State University -- This page last updated Nov 25, 1996

Contents of Network Flow
- Reference
- Network Flow
- The Max-flow min-cut theorem
Chapter 27 of the text
A flow network G = (V, E) is a directed graph where each edge
(u, v)
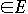 has a capacity c(u, v) >= 0
has a capacity c(u, v) >= 0
Source (s) - node with only outflows
Sink (t) - node with only inflows
Assume graph is connected
Multiple Sources/Sinks
Super Sources and Sinks
A flow in G is a real-valued function f : V * V -> R such that:
- For all u, v
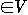 ,
f(u, v) <= c(u, v) [Capacity constraint]
,
f(u, v) <= c(u, v) [Capacity constraint]
-
- For all u, v
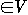 ,
f(u, v) = -f(v, u) [Skew symmetry]
,
f(u, v) = -f(v, u) [Skew symmetry]
-
- For all u
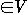 - {s, t},
- {s, t},
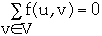 [Flow conservation]
[Flow conservation]
Value of a flow f is
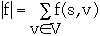
Positive Net Flow entering vertex v is
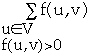
Positive Net Flow leaving vertex v is
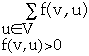
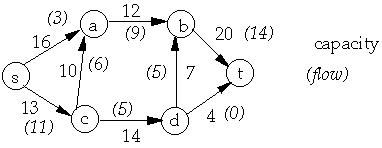
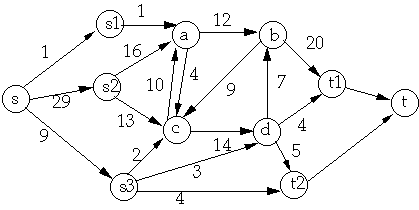
f(a, b) = 9 f(b, a) = -9 c(b, a) = 0 c(a, d) = 0 f(a, d) = 0
Oh Boy More Notation
Implicit Summation Notation
Let
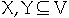 then
then
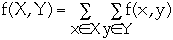
X = {a, c}, Y = {b, d } then
f(X, Y) = f(a, b) + f(a, d) + f(c, b) + f(c, b)
- = 12 + 0 + -9 + 14
-
- = 17
Lemma. Let G = (V, E) be a flow network and f be a flow in G
a. If
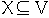 then f(X, X) = 0
then f(X, X) = 0
b. If
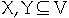 then
f(X, Y) = -f(Y, X)
then
f(X, Y) = -f(Y, X)
c. If
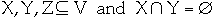 then
then
-
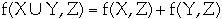 and
and
-
-
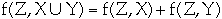
proof of a
- For all u
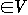 f(u, u) = 0 since we have f(u, u) = -f(u, u)
f(u, u) = 0 since we have f(u, u) = -f(u, u)
-
- We have:
-
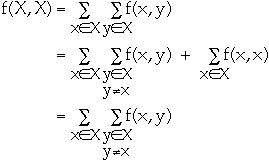
-
- For every term f(x, y) we also have f(y, x)
-
- Since f(x, y) = -f(y, x) we have f(X, X) = 0
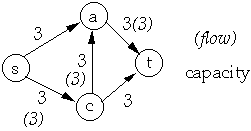
Let G = (V, E) be a flow network and f a flow in G
residual capacity of (u, v) is cf(u, v) = c(u, v) - f(u, v)
residual network of G induced by f is Gf = (V, Ef)
where
- Ef = { (u, v) V * V : cf(u, v) > 0}
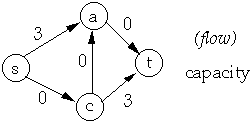
Residual Network
| Network | Flow on Network |
 | 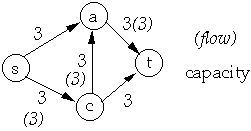 |
| Residual Network | Flow in Residual Network |
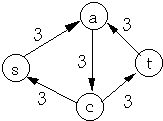 | 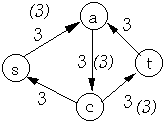 |
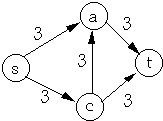
Resultant Flow in Original Network
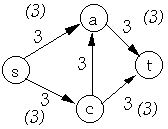
Let G = (V, E) be a flow network and f be a flow in G.
Let Gf = (V, Ef) be the residual network of G induced by
f.
Let h be a flow in Gf.
Define f + h to by (f + h )(u, v) = f(u, v) + h(u, v)
Lemma. f + h is a flow in G with value |f + h|= |f|+|h|
proof of Capacity constraint
- (f + h )(u, v)
- = f(u, v) + h(u, v)
-
-
-
- = -f(v, u) - h(v, u)
-
-
- = -(f(v, u) + h(v, u))
-
-
- = -(f + h )(v, u)
Augmenting Paths
Let G = (V, E) be a flow network and f be a flow in G.
Let Gf = (V, Ef) be the residual network of G induced by
f.
An augmenting path p is a simple path from s to t in Gf
Residual capacity of p is the maximum amount of net flow that we can
ship along the edges of p
cf(p) = min { cf(u, v) : (u, v) is on path p}
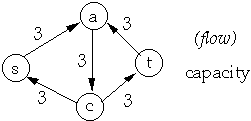
| Residual Network | Flow in Residual Network |
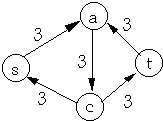 | 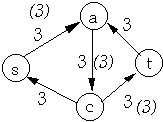 |
Lemma. Let G = (V, E) be a flow network and f be a flow in
G.
Let p be an augmenting path in Gf. Define hp : V * V
-> R by:
-
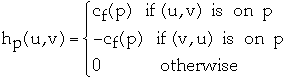
Then hp is a flow in Gf with value
|hp| = cf(p).
Corollary
Let G = (V, E) be a flow network and f be a flow in G.
Let p be an augmenting path in Gf. Define hp as
above.
Let k = f + hp. Then k is a flow in G with value
- |k| = |f|+ | hp | > |f|
Ford-Fulkerson Method to find Maximum Flow
Let G = (V, E) be a flow network
initialize flow f to 0
while there exits an augmenting path p
- do add hp to f
return f
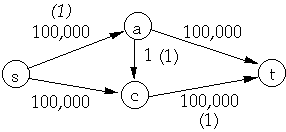
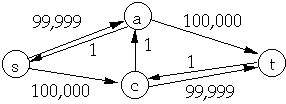
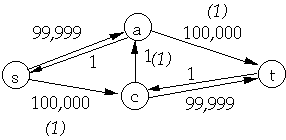
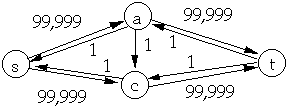
Let G = (V, E) be a flow network and f a flow in G
A cut (S, T) of G is a partition of V into S and T = V - S such that:
-
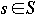 and
and
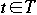
The net flow across the cut (S, T) is f(S, T)
The capacity of the cut (S, T) is c(S, T)
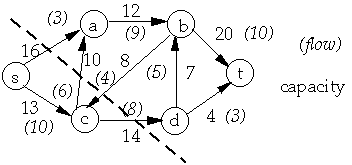
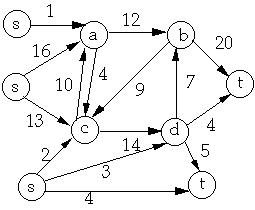
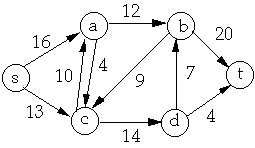
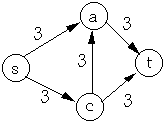
S = {s, c} T = { a, b, d, t}
f(S, T) = 3 + 6 - 4 + 8 = 13
c(S, T) = 16 + 10 + 14
Lemma
Let G = (V, E) be a flow network and f be a flow in G.
Let (S, T) be a cut of G. Then the net flow across (S, T) is
- f(S, T) = |f|
proof:
- f(S, T)
- = f(S, V - S)
-
- = f(S, V) - f(S, S)
-
- = f(S, V)
-
- = f(s, V) + f(S - s, V)
-
- = f(s, V)
-
- = |f|
Corollary The value of any flow f in a flow network G is bounded from
above by the capacity of any cut of G
Let f be a flow in G = (V, E) be a flow network with source s and sink
t.
The following are equivalent:
1. f is a maximum flow in G
2. The residual network Gf contains no augmenting paths
3. |f| = c(S, T) for some cut (S, T) of G.
Ford-Fulkerson Algorithm to find Maximum Flow
Let G = (V, E) be a flow network
for each edge (u, v)
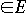 do
do
- f[u, v] = 0
- f[v, u] = 0
while there exits a path p from s to t in residual network Gf
do
- do cf(p) = min { cf(u, v) : (u, v) is on path
p}
- for each edge (u, v) in p
- do
- f[u, v] = f[u, v] + cf(p)
-
-
- f[u, v] = -f[v, u]
return f
How long does it take?
Edmonds-Karp Algorithm
Find shortest path from s to t in Ford-Fulkerson
Let G = (V, E) be a flow network and f be a flow in G.
Let Gf = (V, Ef) be the residual network of G induced by
f.
Let p be shortest path from s to t in Gf.
Define the flow
-
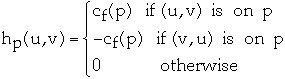
Let df(x, y) be the shortest-path distance from x to y in
Gf
Let dh(x, y) be the shortest-path distance from x to y in
Gh
Lemma 27.8 For all v
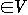 - {s, t} we have df(s, v) <= dh(s, v)
- {s, t} we have df(s, v) <= dh(s, v)
proof:
- Assume that there exists v such that df(s, v) >
dh(s, v)
-
- Let v be the closes vertex to s for which this is true
-
- Let sp be the shortest path from s to v in Gf
-
- Let u be the vertex before v on sp and f[u, v] < c(u,v) then
-
- df(s, v)
- = df(s, u) + 1
- <= dh(s, u) + 1
-
- = dh(s, v)
- So we must have f[u, v] = c(u, v)
-
- Thus (u, v) is not in Ef which means (v, u) is in Ef
-
- So df(s, u)
- = df(s, v) + 1
-
- That is flow goes from v to u
-
- df(s, v)
- = df(s, u) - 1
- <= dh(s, u) - 1
- = dh(s, v) - 2
- < dh(s, v)
Theorem The Edmonds-Karp Algorithm will perform at most O(V*E) flow
augmentations.
proof:
- An edge (u, v) in a residual network Gf is critical on an
augmenting path p if the residual capacity of p is the residual capacity of
(u, v)
-
- How many times can an edge be critical?
-
-
- We have (draw picture)
- df(s, v)
- = df(s, u) + 1
- dh(s, u)
- = dh(s, v) + 1
-
-
- So dh(s, u)
- = dh(s, v) + 1
- >= df(s, v) + 1
- = df(s, u) + 2
-
- Thus ( u, v) can be critical at most O(V) times
Since there are O(E) edges the total number of critical edges is O(E*V)
 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms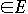 has a capacity c(u, v) >= 0
has a capacity c(u, v) >= 0



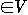 ,
f(u, v) <= c(u, v) [Capacity constraint]
,
f(u, v) <= c(u, v) [Capacity constraint]
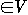 ,
f(u, v) = -f(v, u) [Skew symmetry]
,
f(u, v) = -f(v, u) [Skew symmetry]
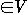 - {s, t},
- {s, t},
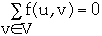 [Flow conservation]
[Flow conservation]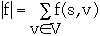
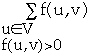
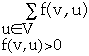

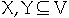 then
then
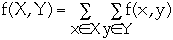

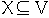 then f(X, X) = 0
then f(X, X) = 0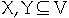 then
f(X, Y) = -f(Y, X)
then
f(X, Y) = -f(Y, X) 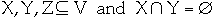 then
then 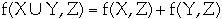 and
and
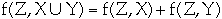
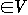 f(u, u) = 0 since we have f(u, u) = -f(u, u)
f(u, u) = 0 since we have f(u, u) = -f(u, u)
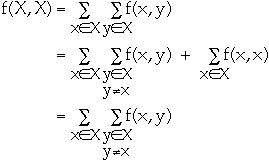









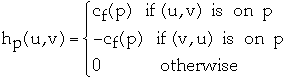





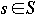 and
and
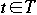

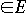 do
do
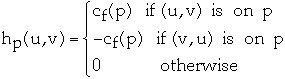
 - {s, t} we have df(s, v) <= dh(s, v)
- {s, t} we have df(s, v) <= dh(s, v)