 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms
Review of Mathematical Analysis of Algorithms
[To Lecture Notes Index]
San Diego State University -- This page last updated 8/29/95

Contents of Intro Lecture
- References
- Mathematical Analysis of Algorithms
- Model of Computing
- Asymptotic Notation
- Timing Analysis
- Timing in C on Rohan
- Handling Measurement Errors1
- Estimating Complexity from Timing Results
- Mathematical Analysis and Timing Code
Introduction To Algorithms, Corman, Leiserson,Rivest, Chapters 1-4
If analysis of algorithms is the answer, what is the question?
Given two or more algorithms for the same task, which is better?
- Under which condition is bubble sort better than insertion sort?
What computing resources does an algorithm require?
- How long will it take bubble sort to sort a list of N items?
Goal of mathematical analysis is a function of the resources required of an
algorithm
On what computer?
What is a Computer?
Random-access machine (RAM)
- Single processor
- Instructions executed sequentially
- Each operation requires the same amount of time
-
Single cost vs. Lg(N) cost
- Time required for basic operation?
-
- 3 + 6
- 1234!
Insertion Sort
A[0] = - infinity
for K = 2 to N do
begin
- J = K;
- Key = A[J];
- while Key < A[J-1] do
- begin
A[J] = A[J-1];
J = J - 1;
- end while;
- A[J] = Key;
end for;
Complexity
- Resources required by the algorithm as a function of the input
size
Worst-case Analysis
- Complexity of an algorithm based on worst input of each size
Average-case Analysis
- Complexity of an algorithm averaged over all inputs of each size
-
Insertion Sort
| Comparisons | Element moves |
| worst case | (N+1)N/2 - 1 | (N-1)N/2 |
| average case | (N+1)N/4 - 1/2 | (N-1)N/4 |
Asymptotically tight bound
-
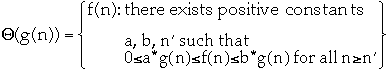
-
-
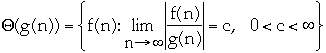
Asymptotic upper bounds
-
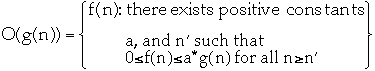
-
-
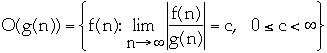
Common Myths and Errors
- Everyone incorrectly writes:
-
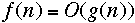
- instead of:
-
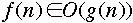
-
- or even that there is an n such that
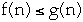
- Let f(n) = 2n + 10, and g(n) = n then
-
- f(n) = O(g(n)) but f(n) > g(n)
- Using O( ) when mean
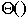
Bubble vs. Insertion Sort
| Worst case | Average case |
| Bubble sort | | |
| Insertion Sort | | |
Bubble Sort
| Comparisons | Element moves |
| worst case | (N-1)N/2 | 3(N-1)N/2 |
| average case | (N-1)N/2 | 3(N-1)N/4 |
| best case | (N-1)N/2 | 0 |
Insertion Sort
| Comparisons | Element moves |
| worst case | (N+1)N/2 - 1 | (N-1)N/2 |
| average case | (N+1)N/4 - 1/2 | (N-1)N/4 |
| best case | N - 1 | 0 |
Bubble vs. Insertion SortTiming Results
Worst Case
| N | Bubble | Insertion |
| 100 | 1 | 1 |
| 200 | 5 | 3 |
| 400 | 19 | 11 |
| 800 | 79 | 42 |
| 1600 | 317 | 166 |
Average Case
| N | Bubble | Insertion |
| 100 | 1 | 0 |
| 200 | 3 | 1 |
| 400 | 14 | 5 |
| 800 | 56 | 21 |
| 1600 | 228 | 84 |
What is wrong with this Picture?
main()
{
- int k, iterations;
- for (iterations = 0; iterations < 50; iterations++)
- {
- start();
- /* start the timer */
- for (k = 0; k < 2000000; k++)
- /* do some work */
- k = k;
- stop();
- /* stop the timer */
-
- printf("Time taken: %ld\n", report());
- };
}
Result on Rohan
Time Frequency Occurred
30 2
31 2
32 9
33 10
34 11
35 9
36 5
37 1
39 1
Source for Timing C Code on Rohan
#include <stdio.h>
#include <sys/times.h>
#include <limits.h>
static struct tms _start; /* Stores the starting time*/
static struct tms _stop; /* Stores the ending time*/
int start()
{
times(&_start);
}
int stop()
{
times(&_stop);
}
unsigned long report()
{
return _stop.tms_utime - _start.tms_utime;
}
main()
{
int k, iterations;
- for (iterations = 0; iterations < 50; iterations++)
- {
- start();
- /* start the timer */
-
- for (k = 0; k < 2000000; k++)
- /* do some work */
- k = k;
-
- stop();
- /* stop the timer */
-
- printf("Time taken: %ld\n", report());
- };
}
Repeat a measurement n times
Let the measurements be labeled
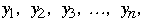
Let
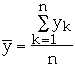 and
and
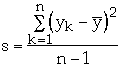
The confidence interval for the true measurement is[2]:
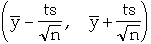
The value of t determine the probability the measurement is in the interval
When n >= 50
Probability
| 50% | 80% | 90% | 95% | 99% |
value of t
| 0.67 | 1.28 | 1.64 | 1.96 | 2.58 |
In Example
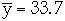 ,
s = 3.15, selecting t = 1.96 we get
,
s = 3.15, selecting t = 1.96 we get
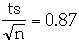
95% confidence interval is (32.83, 34.57)
Student t table - When n < 50
| n | 90% | 95% | 99% |
| 1 | 3.078 | 6.314 | 31.821 |
| 2 | 1.886 | 2.920 | 6.965 |
| 3 | 1.638 | 2.353 | 4.541 |
| 4 | 1.533 | 2.132 | 3.747 |
| 5 | 1.476 | 2.015 | 3.365 |
| | | |
| 6 | 1.440 | 1.943 | 3.143 |
| 7 | 1.415 | 1.895 | 2.998 |
| 8 | 1.397 | 1.860 | 2.896 |
| 9 | 1.383 | 1.833 | 2.821 |
| 10 | 1.372 | 1.812 | 2.764 |
| | | |
| 20 | 1.325 | 1.725 | 2.528 |
| 30 | 1.310 | 1.697 | 2.457 |
| 40 | 1.303 | 1.684 | 2.423 |
Fun with Functions
Let f(n) = 3n*n + 4n + 5 and g(n) = 3n*n
Fact: g(n) is an approximation of f(n)
Notation: f(n) = g(n) +
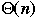
| n | f(n) | g(n) | % error |
| 1 | 12 | 3 | 75.00% |
| 10 | 345 | 300 | 13.04% |
| 20 | 1285 | 1200 | 6.61% |
| 30 | 2825 | 2700 | 4.42% |
| 40 | 4965 | 4800 | 3.32% |
| 50 | 7705 | 7500 | 2.66% |
| 60 | 11045 | 10800 | 2.22% |
| 70 | 14985 | 14700 | 1.90% |
| 80 | 19525 | 19200 | 1.66% |
| 90 | 24665 | 24300 | 1.48% |
| 100 | 30405 | 30000 | 1.33% |
| 200 | 120805 | 120000 | 0.67% |
| 300 | 271205 | 270000 | 0.44% |
Eyeballing Complexity
Let
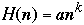 then
then
-
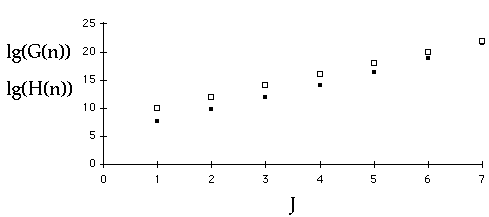
Timing Results
| N | Bubble | Insertion |
| 100 | 1 | 1 |
| 200 | 5 | 3 |
| 400 | 19 | 11 |
| 800 | 79 | 42 |
| 1600 | 317 | 166 |
Plotting Complexity
Cubic or Quadratic[3]?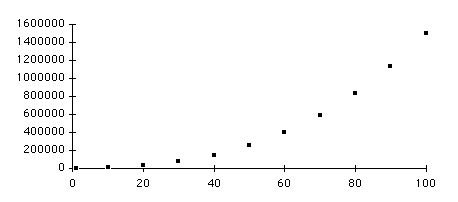
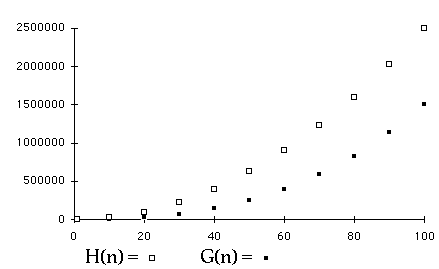 Plotting ComplexityEngineers Method (Modified)
Plotting ComplexityEngineers Method (Modified)
Let
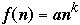 then
then
-
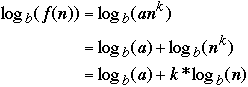
Let b = 2 and
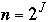 then
then
-
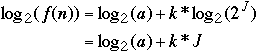
 Plotting ComplexityTransform the Axis
Plotting ComplexityTransform the Axis
Let
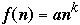 and
and
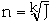 (or
(or
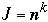 )
then:
)
then:
g(J) = f(
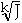 )
= a(
)
= a(
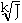 )k
= aJ
)k
= aJ
So g(J) is linear!
Example
| n | f(n) =5n*n+n + 3 | J=n*n |
| 1 | 9 | 1 |
| 10 | 513 | 100 |
| 20 | 2023 | 400 |
| 30 | 4533 | 900 |
| 40 | 8043 | 1600 |
| 50 | 12553 | 2500 |
| 60 | 18063 | 3600 |
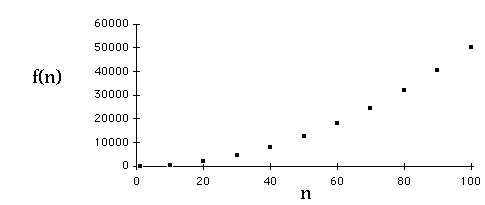
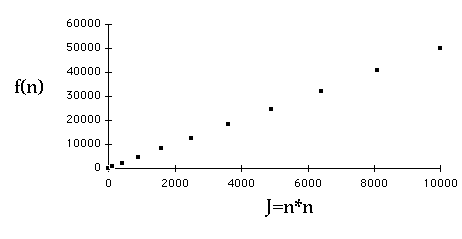 Which is Quadratic?
Which is Quadratic?
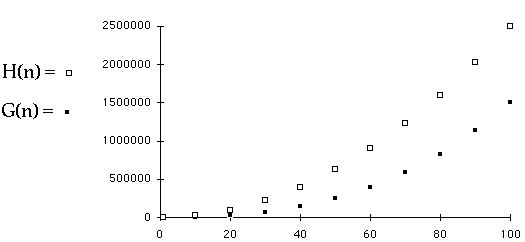
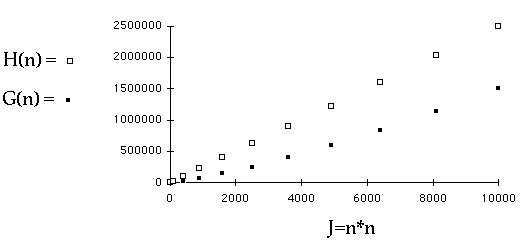
Bubble sort worst case is
 (
n*n )
(
n*n )
Complexity is an*n + bn + c
Timing Results Worst Case
| N | Bubble Sort |
| 400 | 20 |
| 500 | 31 |
| 600 | 45 |
| 700 | 61 |
| 800 | 79 |
Least Squares fit of data to an*n + bn + c
Bubble sort worst case is 0.0001143n*n + 0.01084n - 2.738
Predicted vs. Actual Time for Bubble Sort
| N | Actual | Predicted | % Error |
| 900 | 105 | 99.601 | 5.14% |
| 1000 | 124 | 122.402 | 1.29% |
| 1100 | 149 | 147.489 | 1.01% |
| 2000 | 496 | 476.142 | 4.00% |
| 2400 | 713 | 681.646 | 4.40% |
 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms