SDSU CS 660: Combinatorial Algorithms
Amortized Analysis

[To Lecture Notes Index]
San Diego State University -- This page last updated September 12, 1995
----------

Contents of Amortized Analysis Lecture

  1. Reference
  2. Amortized Analysis
    1. Aggregate Method
    2. Accounting Method
    3. Potential Method

Reference

Introduction to Algorithms by Cormen, Leiserson, Rivest. Chapter 18

Amortized Analysis


In a sequence of operations on a data structure often the worst case can not occur in each operation

Example - Move-to-Front

Assume we have a list of n = 2k items: a1, a2, ..., an

Will perform n accesses on the list

Will access item a1 n/2 times


Worst case access requires n compares

Thus worst case cost for n access is O(n*n)?????


At most 1 + n/2 accesses require n comparisons!


Once item a1 is accessed it will not make it to the end of the list



Amortized Analysis gives the average performance of each operation in the worst case
Example - Incrementing a k-bit binary counter

Let A[0..k-1] be an array of bits representing a number X

A[0] - low order bit, so
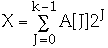
length[A] = k

Start with X = 0

Increment (A)
J = 0
while J < length[A] and A[J] == 1 do
A[J] = 0
J = J + 1
end while
if J < length[A] then
A[J] = 1
end if
end Increment

Count bits flipped

Worst Case
Increment flips k bits in worst case
Sequence of n Increment operations takes O(nk)

Aggregate Method


T(n) = all work done in worst case in sequence of n operations

Amortized cost per operation is T(n)/n
	X	A[4]	A[3]	A[2]	A[1]	A[0]	Total Cost
	0	0	0	0	0	0	0
	1	0	0	0	0	1	1
	2	0	0	0	1	0	3
	3	0	0	0	1	1	4
	4	0	0	1	0	0	7
	5	0	0	1	0	1	8
	6	0	0	1	1	0	10
	7	0	0	1	1	1	11
	8	0	1	0	0	0	15
	9	0	1	0	0	1	16

A[0] flips each time Increment is called n
A[1] flips every other time
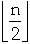
A[1] flips every fourth time
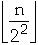
A[J] flips every 2**J time
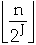
Total number of flips is:

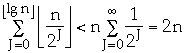
So amortized cost of each operation is 2 = O(1)

Accounting Method


Assign an amortized cost to each operation

Amortized cost may be more or less than the actual cost

If amortized cost is more than the actual cost of the operation assign the difference to part of the data structure as a credit

No negative credit allowed

Total amortized cost is >= total worst case cost

Example - binary counter

Amortized cost of setting bit to 1 2 units
1 unit to pay for setting bit to 1
1 unit stored with bit

Amortized cost of setting bit to 0 0 units
Only a 1-bit is set to 0,
All 1-bits have credit of one unit
This pays for setting bit to 0
Increment (A)
	J = 0
	while J < length[A] and A[J] == 1  do 
		A[J] = 0							Cost 0
		J = J + 1
	end while

	if J < length[A] then
		A[J] = 1							Cost 2
	end if
end Increment

	X	A[4]	A[3]	A[2]	A[1]	A[0]	Amortized cost
	0	0	0	0	0	0	0
	1	0	0	0	0	1 (1)	2
	2	0	0	0	1 (1)	0	4
	3	0	0	0	1 (1)	1 (1)	6
	4	0	0	1 (1)	0	0	8
	5	0	0	1 (1)	0	1 (1)	10
	6	0	0	1 (1)	1 (1)	0	12
	7	0	0	1 (1)	1 (1)	1 (1)	14
	8	0	1 (1)	0	0	0	16
	9	0	1 (1)	0	0	1 (1)	18
Example - Move-to-Front

Assume we have a list of n = 2k items: a1, a2, ..., an

Will perform n accesses on the list

Will access item a1 n/2 times

Amortized costs:
First access of a
initial location of a <= n
All other access of a
1
Accessing a non-a item
actual cost + 1 <= n +1
assign credit to a 
a,	b,	c,	d,	e		Amortized cost
b,	a(1),	c,	d,	e	accessed b 	2
c,	b,	a(2),	d,	e	accessed c	4
a,	c,	b,	d,	e	accessed a	1
e	a(1),	c,	b,	d	accessed e	6
a,	c,	b,	d,	e	accessed a	1
a,	c,	b,	d,	e	accessed a	1

(Amortized cost of all accesses of a) <= n + n/2 - 1 = 3n/2 - 1

(Amortized cost of accessing all non-a items) <= n*(n+1)/2

(Total Cost) <= (4n + n*n)/2 -1, (Average Cost/access) <= 4 + n/2

Potential Method


Assign an amortized cost to each operation

Amortized cost may be more or less than the actual cost

If amortized cost is more than the actual cost of the operation assign the difference the entire data structure as potential energy

ck= actual cost of operation k

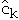= amortized cost of operation k

Dk = the state of the data structure after applying k'th operation to Dk

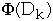= potential associated with Dk




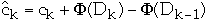
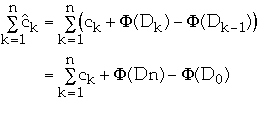
So if 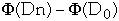>=0 then 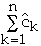is an upper bound on total cost of the algorithm
Example - binary counter

Potential = number of 1's in the counter

if the k'th operation sets tk bits to 0 the actual cost is tk + 1

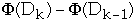=1 - tk

so

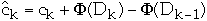= 2



How to find ?
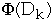Dynamic Tables

Table -> pointer to a table

Number -> number of items in the table

Size -> size of the table


AddToTable(x)
if Number == Size then
allocate NewTable with size 2*Size
insert all items from Table to newTable
free Table
Table = NewTable
Size = 2 * Size
end if
insert x into Table
Number = Number + 1
end insert
How many inserts are done by N AddToTable?


Amortized Cost per AddToTable 3 inserts


Table after moving from size 4 to size 8

Perform 4 AddToTable operations

	X	X	X	X								
	
	X	X	X	X	Y(2)						
	
	X	X	X	X	Y(2)	Y(2)				
	
	X	X	X	X	Y(2)	Y(2)	Y(2)		
	
	X	X	X	X	Y(2)	Y(2)	Y(2)	Y(2)



1/2 the table has 2 credits

One credit per item to pay for the move to next size table

X	X	X	X	Y	Y	Y	Y
Table Expansion and Contraction

Policy
When table becomes full move to table twice the size
When table contracts to 1/4 full, move to table 1/2 size


Let load = (Size of table) / (number of items in the table)


Amortized Cost
Inserting when load >= 1/2
3 units
Inserting when load < 1/2
0 units
Deleting when load > 1/2
0 units
Deleting when load <= 1/2
2 units
	X	X	X	X								
	X	X	X	X	Y(2)						
	X	X	X	X								
	X	X	X	(1)								
	X	X	(1)	(1)								
	X	X
Linked List vs. Dynamic Array
Unordered List

Amortized Costs per operation over n operations
			linked List	Dynamic Array
	
	Insertion	1 call to new	lg(n)/n call to new
	
			set two links	3 data moves
	

Deletion after find	two links	3 data moves
	
			1 delete	lg(n)/n call to new