SDSU CS 660: Combinatorial Algorithms
Red-Black and B trees

[To Lecture Notes Index]
San Diego State University -- This page last updated October 21, 1995
----------

Contents of Red-Black and B trees Lecture

  1. Balanced Trees
    1. Red-Black Trees
      1. Inserting in Red-Black Tree
      2. Deleting in a Red-Black Tree
    2. B-Trees, (a,b)-Trees
      1. Insertion in a B-Tree
      2. Deletion in a B-Tree
      3. B-Trees and Red-Black Trees

Balanced Trees

Red-Black Trees


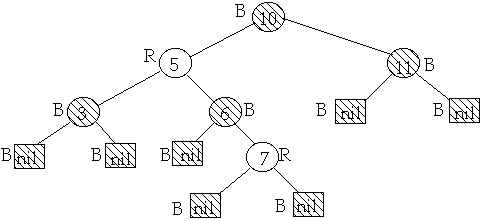
A binary search tree is a red-black tree if:
1. Every node is either red or black
2. Every leaf (nil) is black
3. If a node is red, then both its children are black
4. Every simple path from a node to a descendant leaf contains the same number of black nodes

Black-height of a node x, bh(x), is the number of black nodes on any path from x to a leaf, not counting x



Lemma
A red-black tree with n internal nodes has height at most 2lg(n+1)


proof
Show that subtree starting at x contains at least 2bh(x)-1 internal nodes. By induction on height of x:
if x is a leaf then bh(x) = 0, 2bh(x)-1
Assume x has height h, x's children have height h -1
x's children black-height is either bh(x) or bh(x) -1
By induction x's children subtree has 2bh(x)-1-1 internal nodes
So subtree starting at x contains
2bh(x)-1-1 + 2bh(x)-1-1 + 1 = 2bh(x)-1 internal nodes
let h = height of the tree rooted at x
bh(x) >= h/2
So n >= 2h/2-1 <=> n + 1 >= 2h/2 <=> lg(n+1) >= h/2
h <= 2lg(n+1)

Inserting in Red-Black Tree


Color the node Red
Insert as in a regular BST
If have parent is red
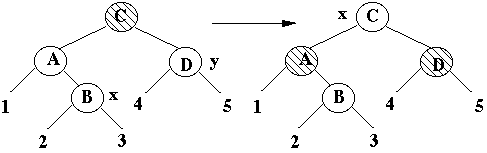
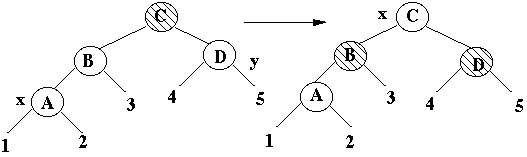
Case 1

x is node of interest, x's uncle is Red



Decrease x's black height by one
Case 2

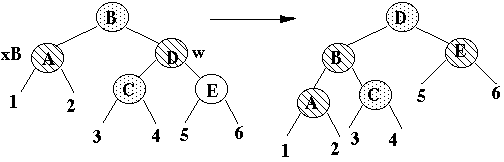
x's uncle is Black, x is a Right child



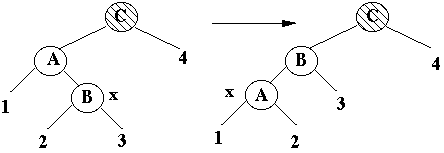
Transform to case 3

Case 3

x's uncle is Black, x is a Left child


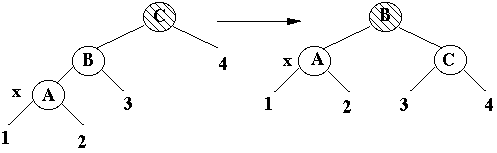
Terminal case, tree is Red-Black tree


Insertion takes O(lg(n)) time
Requires at most two rotations

Deleting in a Red-Black Tree


Find node to delete
Delete node as in a regular BST
Node to be deleted will have at most one child

If we delete a Red node tree still is a Red-Black tree
Assume we delete a black node

Let x be the child of deleted node
If x is red, color it black and stop

If x is black mark it double black and apply the following:
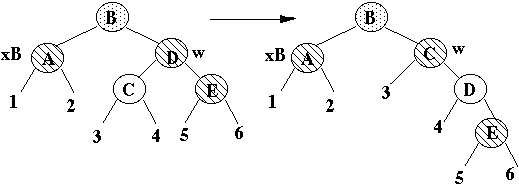
Case 1

x's sibling is red


x stays at same black height
Transforms to case 2b then terminates
Case 2a

x's sibling is black
x's parent is black



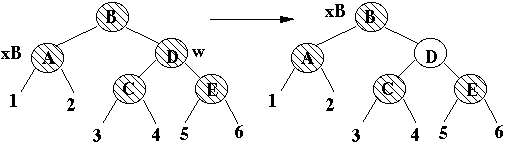
Decreases x black height by one
Case 2b

x's sibling is black
x's parent is red


Terminal case, tree is Red-Black tree
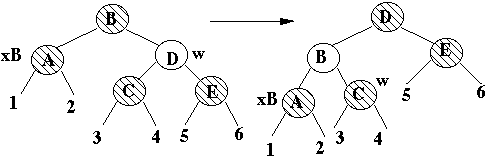
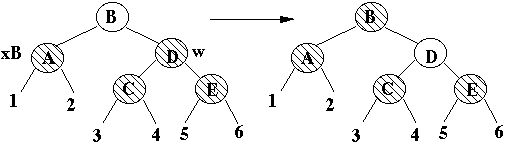
Case 3

x's sibling is black
x's parent is either
x's sibling's left child is red
x's sibling's right child is black

x stays at same black height
Transforms to case 4
Case 4

x's sibling is black
x's parent is either
x's sibling's left child is either
x's sibling's right child is red



Terminal case, tree is Red-Black tree



Delete time is O(lg(n))
At most three rotations are done

B-Trees, (a,b)-Trees


(a,b)-Trees

Let a and b be integers with a >= 2 and 2a-1 <= b. A tree T is an (a,b)-tree if

a) All leaves of T have the same depth

b) All internal nodes v of T satisfy c(v) <= b

c) All internal nodes v of T except the root satisfy c(v) >= a

d) The root of T satisfies c(v) >= 2

c(v) = number of children of node v


B-Trees of degree t

A tree T is a B-Trees of degree t if

a) All leaves of T have the same depth

b) All nodes of T except the root have at least t-1 keys

c) All nodes of T except the root have at most 2t-1 keys

d) The root of T at least one key

e) A node with n keys has n+1 children

c(v) = number of children of node v

 Theorem. If n >= 1, then for any n-key B-tree T of height h and degree t >= 2 then

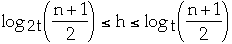
proof.
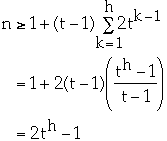
so

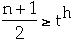
take log of both sides.

Theorem. The worst case search time on a n-key B-tree T of degree t is O(lg(n)).
A node in T has t-1 <= K <= 2t-1 keys in sorted order.
Worst case:
K = t-1 for all nodes
searching for X not in the tree
Given a node, W, in T, how much work does it take to find the subtree of W that would contain X?
Using binary search it takes
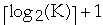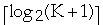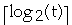= = comparisons
Since the height of the tree is in worst case 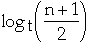the total amount of work is:

Insertion in a B-Tree

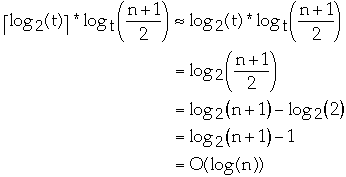
Inserting X into B-tree T of degree t

A full node is one that contains 2t-1 keys

1. Find the leaf that should contain X

2. If the path from the root to the leaf contains a full node split the node when you first search it.
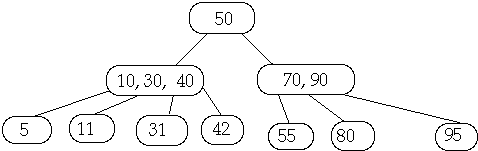
Example t = 2, Insert 25
Full Node is split, Then insert 25 into subtree b

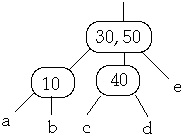
3. Insert X into the proper leaf
Example t = 2, Insert 25

Deletion in a B-Tree

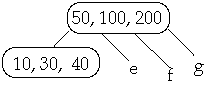
Deleting X from B-tree T of degree t

A minimal node is one that contains t-1 keys and is not the root

In the search path from the root to node containing X, if you come across a minimal node add a key to it.


Case 3. Searching node W that does not contain X. Let c be the child of W that would contain X.

Case 3a. if c has t-1 keys and a sibling has t or more keys, steal a key from the sibling
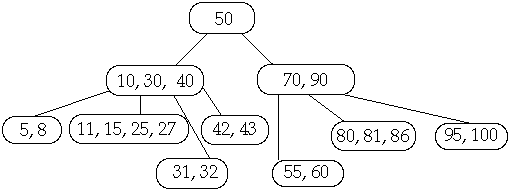
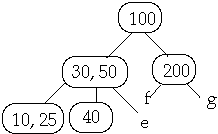
Example t = 2, Delete 250

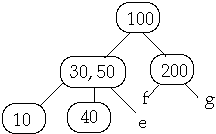
Case 3b. if c has t-1 keys and all siblings have t-1 keys, merge c with a sibling
Example 1. t = 2, Delete 250
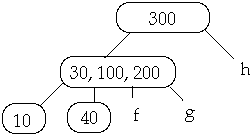Example 2. t = 2, Delete 250
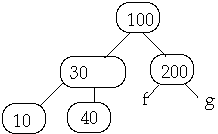
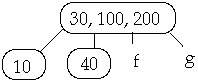Case 2. Internal node W contains X.

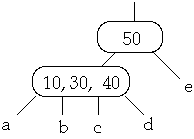
Case 2a. If the child y of W that precedes X in W has at least t keys, steal predecessor of W
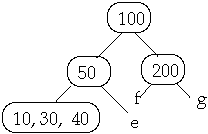
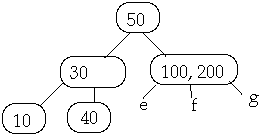
Example 1. t = 2, Delete 50
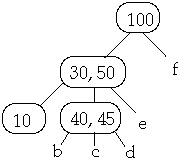Now Delete 45w
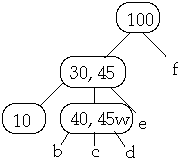Case 2b. If the child z of W that succeed X in W has at least t keys, steal the successor of W
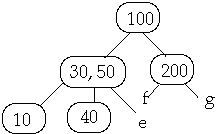
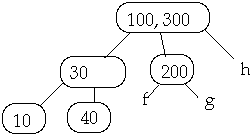
Example 1. t = 2, Delete 30
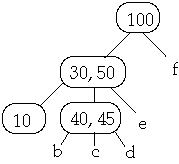Now Delete 40w
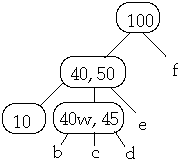Case 2c. If both children z and y of W that succeed (follow) X in W have only t-1 keys, merge z and y
Example t = 2, Delete 30
Now Delete 30w one lower level

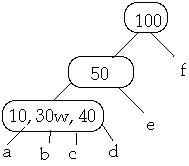
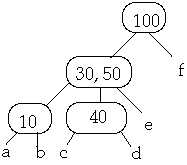
Case 1. X is in node W a leaf. By case 3, W has at least t keys. Remove X from W

B-Trees and Red-Black Trees


Theorem. A Red-Black tree is a B-Tree with degree 2

proof:

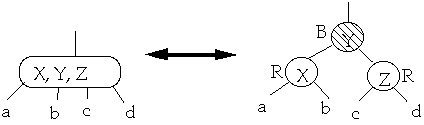
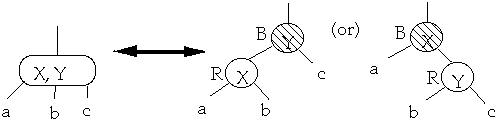
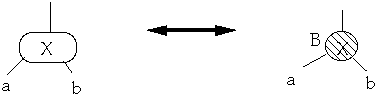
Must show:
1. If a node is red, then both its children are black
2. Every simple path from a node to a descendant leaf contains the same number of black nodes