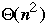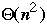CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms
Introduction Part A
[To Lecture Notes Index]
San Diego State University -- This page last updated Septemper 3, 1995

Contents of Introduction Part A Lecture
- References
- Mathematical Analysis of Algorithms
- Model of Computing
- Asymptotic Notation
Introduction To Algorithms, Corman, Leiserson,Rivest, Chapters 1-4
If analysis of algorithms is the answer, what is the question?
Given two or more algorithms for the same task, which is better?
- Under which condition is bubble sort better than insertion sort?
What computing resources does an algorithm require?
- How long will it take bubble sort to sort a list of N items?
Goal of mathematical analysis is a function of the resources required of an
algorithm
On what computer?
What is a Computer?
Random-access machine (RAM)
- Single processor
- Instructions executed sequentially
- Each operation requires the same amount of time
-
Single cost vs. Lg(N) cost
- Time required for basic operation?
-
- 3 + 6
- 1234!
Insertion Sort
A[0] = - infinity
for K = 2 to N do
begin
- J = K;
- Key = A[J];
- while Key < A[J-1] do
- begin
A[J] = A[J-1];
J = J - 1;
- end while;
- A[J] = Key;
end for;
Complexity
- Resources required by the algorithm as a function of the input
size
Worst-case Analysis
- Complexity of an algorithm based on worst input of each size
Average-case Analysis
- Complexity of an algorithm averaged over all inputs of each size
-
Insertion Sort
Comparisons Element moves
worst case (N+1)N/2 - 1 (N-1)N/2
average case (N+1)N/4 - 1/2 (N-1)N/4
Asymptotically tight bound
-
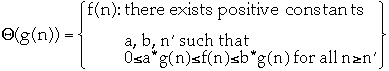
-
-
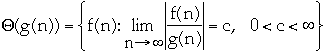
Asymptotic upper bounds
-
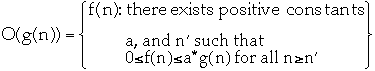
-
-
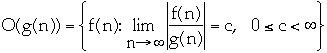
Common Myths and Errors
- Everyone incorrectly writes:
-
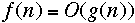
- instead of:
-
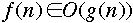
-
- or even that there is an n such that
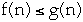
- Let f(n) = 2n + 10, and g(n) = n then
-
- f(n) = O(g(n)) but f(n) > g(n)
- Using O( ) when mean
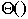
Bubble vs. Insertion Sort
Worst case Average case
Bubble sort 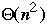
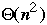 Insertion Sort
Insertion Sort 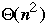
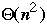
Bubble Sort
Comparisons Element moves
worst case (N-1)N/2 3(N-1)N/2
average case (N-1)N/2 3(N-1)N/4
best case (N-1)N/2 0
Insertion Sort
Comparisons Element moves
worst case (N+1)N/2 - 1 (N-1)N/2
average case (N+1)N/4 - 1/2 (N-1)N/4
best case N - 1 0
Bubble vs. Insertion SortTiming Results
Worst Case
N Bubble Insertion
100 1 1
200 5 3
400 19 11
800 79 42
1600 317 166
Average Case
N Bubble Insertion
100 1 0
200 3 1
400 14 5
800 56 21
1600 228 84
What is wrong with this Picture?
 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms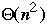
Insertion Sort