 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms
BB[ alpha ] trees
[To Lecture Notes Index]
San Diego State University -- This page last updated October 24, 1995

Contents of BB[ alpha ] trees Lecture
- Reference
- Weight-Balanced Trees
- Rotations and Root Balance
- Performance
Mehlhorn, Data Structures and Algorithms 1: Sorting and Searching, pages
189-199
Let Alpha be a real such that 1/4 < Alpha <= 1 -
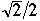
Let T be a binary search tree
Let Tl (Tr ) be the left (right) subtree of the root of T
Definitions
The root balance of T, Rho , is given by:
- Rho(T) = | Tl | / |T | = 1 - | Tr | / | T |
where | T | = number of leaves of tree T
A tree T is of bounded balance Alpha ,
if for every subtree T' of T we have:
- Alpha <= Rho(T' ) <= 1 - Alpha
BB[ Alpha ] is the set of all trees of bounded balance
Alpha
Example of BB[ Alpha ] tree
Alpha <= 1/3
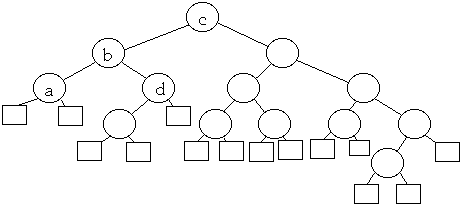
| Node | Root balance |
| a | 1/2 |
| b | 2/5 |
| c | 5/14 |
| d | 2/3 |
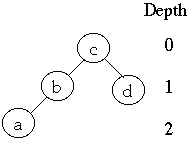
Let
bi denote the depth of node xi in tree T. The average path length of T is
given by:
-
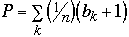
Theorem 2[1] Let T be a BB[
Alpha ] with n nodes. Then
a)
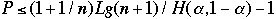
-

b)
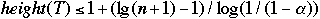
if
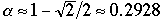 then theorem 2 states
then theorem 2 states
- P <= 1.15(1 + 1/n) lg( n+1) - 1
and
- height(T) <= 2 lg( n +1 ) - 1
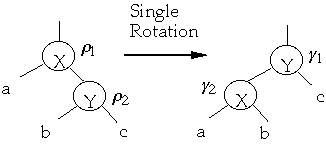
Let a, b ,c denote the number of leaves in the subtrees shown above.
Let
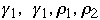 denote the root balance of the subtrees indicated above. We have by
definition:
denote the root balance of the subtrees indicated above. We have by
definition:
-
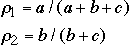
So:
-
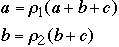
This gives:
-
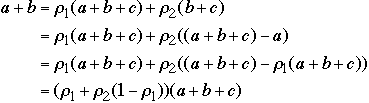
Using the above we get
-
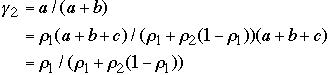
and
-
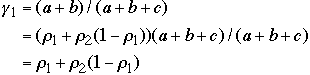
Thus
-
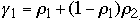
-
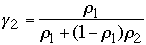
Rotations and Root Balance
Double Rotation
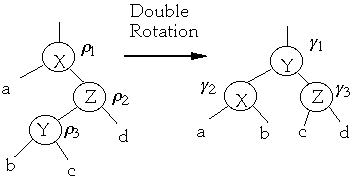
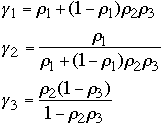
Lemma
- Let
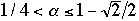 .
.
- Let T' be a BB[ Alpha ] tree.
- Let T be result of adding (deleting) a node from T'.
- Assume that Tl and Tr are BB[ Alpha ] trees.
- Assume that T is no longer a BB[ Alpha ] tree.
- Then a single or double rotation will balance T
Theorem.
- Let
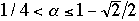 .
Then there is a constant c such that the total number of single and double
rotations required in a sequence of M insertions and deletions into an empty
BB[ Alpha ] tree is <= cM
.
Then there is a constant c such that the total number of single and double
rotations required in a sequence of M insertions and deletions into an empty
BB[ Alpha ] tree is <= cM
For = 3/11 the prove gives the value of c = 19.59
Experiments suggest that c is near 1
Theorem.
- Let
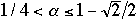 .
Then insert, access, delete takes O(N) in a BB[ Alpha ] tree with N
leaves
.
Then insert, access, delete takes O(N) in a BB[ Alpha ] tree with N
leaves
 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms