CS 660: Combinatorial Algorithms
AVL TREES
[To Lecture Notes Index]
San Diego State University -- This page last updated October 27, 1995
Contents of AVL TREES Lecture
- Height-Balanced Trees
- Insertion into a AVL Tree
- Insertion into a AVL Tree
- Performance
Height of a tree is the length of the longest path from the root to a leaf.
A binary search tree T is a height-balanced k-tree or HB[k]-tree, if each node
in the tree has the HB[k] property
A node has the HB[k] property if the height of the left and right subtrees of
the node differ in height by at most k.
A HB[1] tree is called an AVL tree.
Adel'son-Vel'skii and Landis first defined HB[1] trees
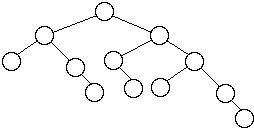
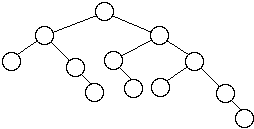
Worst Case AVL Trees
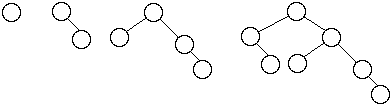
Let
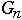= the number of nodes in worst case AVL tree of height n
We have:
-
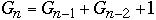
Fibonacci Numbers
,
,
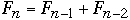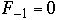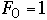
| n |  |  |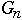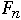
| 0 | 1 | 1 |
| 1 | 2 | 1 |
| 2 | 4 | 2 |
| 3 | 7 | 3 |
| 4 | 12 | 5 |
| 5 | 20 | 8 |
| 6 | 33 | 13 |
We get
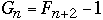
But
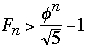where
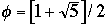
So
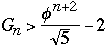
Now take any AVL tree of height h with M nodes, we have
M >=
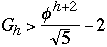
So M + 2 >
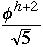
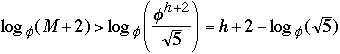
h < 1..4404 lg(M + 2) - 0.328
Theorem ( Adel'son-Vel'skii and Landis 1962) The height of a balanced
tree with N internal nodes always lies between lg (N +1 ) and 1..4404 lg(M + 2)
- 0.328
Case 1
Add node to subtree 3
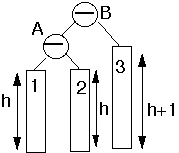
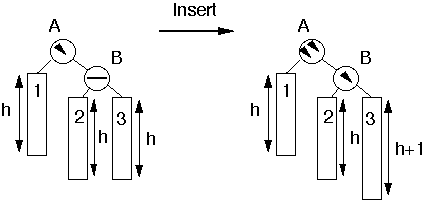Perform Single Rotation
Case 2
Insert into subtree 2 or 3
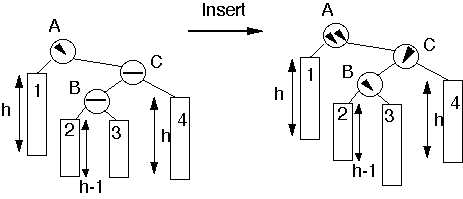
Double Rotation
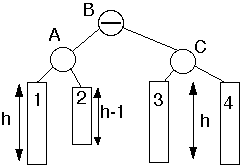
Theorem. An insertion into an AVL tree requires at most one rotation to
rebalance a tree. A deletion may require lg(N) rotations to rebalance the
tree.
Simulation Results
| n | C(n) | E[ h(n) ] | R(n) |
| 5 | 2.2 | 3.0 | 0.213 |
| 10 | 2.907 | 4.0 | 0.318 |
| 50 | 4.930 | 6.947 | 0.427 |
| 100 | 5.889 | 7.999 | 0.444 |
| 500 | 8.192 | 10.923 | 0.461 |
| 1000 | 9.202 | 11.998 | 0.463 |
| 5000 | 11.555 | 14.936 | 0.465 |
| 10000 | 12.568 | 15.996 | 0.465 |
n
= number of nodes in the tree
C(n) = average number of comparisons to find a key
E[ h(n) ] = expected height of tree
R(n) = average number of rotations per insertion/deletion