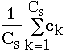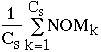CS696: Doc 8, Metrics part 2

CS 696: Advanced OO
Spring Semester, 1997
Doc 8, Metrics part 2

To Lecture Notes Index
San Diego State University -- This page last updated Feb 25, 1997

Contents of Doc 8, Metrics part 2

McCabe's Cyclomatic Complexity	slide # 2
Henderson-Sellers' Recommended OO Metric Suite	slide # 4
...Inside a class	slide # 4
...Metrics External at the Class level	slide # 6
...System Level but Ignoring Relationships - Metrics	slide # 7
...System-Level Relationships but Excluding Inheritance	slide # 8
...Inheritance Coupling	slide # 9

Doc 8, Metrics part 2 Slide # 1

References

Henderson-Sellers, 1996, Object-Oriented Metrics: Measures of Complexity, Prentice Hall

Doc 8, Metrics part 2 Slide # 2

McCabe's Cyclomatic Complexity

Logic Structure Metric

Let G be a connected, directed acyclic graph (DAG) with e edges and n nodes

The cyclomatic complexity (or cycle rank) of G is defined as:

V(G) = e - n + 2

Doc 8, Metrics part 2 Slide # 3

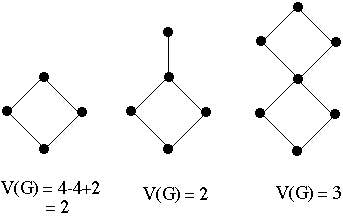
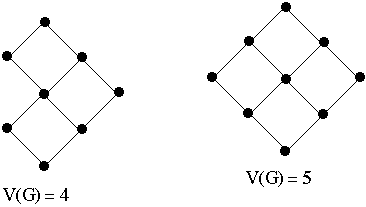
Cyclomatic Complexity and Code Complexity

if ( A< B ) then

W;
else

X;
endif
A = 3;

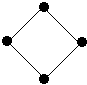
V(G) = 2

if ( A< B ) then 

W;
else 

if ( B < C ) then

X;
else

Z;
endif
endif

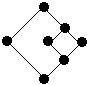
V(G) = 3

switch( A )

case 1: X; break;
case 2: Y; break;
case 3: Z; break;
end case

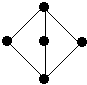
V(G) = 3

Doc 8, Metrics part 2 Slide # 4

Henderson-Sellers' Recommended OO Metric Suite

Inside a class

Assume that a class has:

n public methods

m public data members

r private methods

s private data members

Control Flow Complexity

For each class compute:

V(G) for each of the n + r methods
A distribution of the n + r values of V(G)
A median of the n + r values of V(G)
A mean value of the n + r values of V(G)
A standard deviation of the n + r values of V(G)
A class total V(G)

Note the class total for V(G) is one interpretation of WMC

Doc 8, Metrics part 2 Slide # 5

Inside a class - Metrics

Method Size

For each class compute:

Size of each method (SLOC)
A distribution of the method sizes of a class
A median of the method sizes of a class
A mean value of the method sizes of a class
A standard deviation of the method sizes of a class
A class total method size (TMS)

Class Size

A class total number of all methods (NOM)
A class total number of attributes (data members) (NOA)
Weighted class size = NOA + TMS
Unweighted class size = NOA + NOM

Other Class Metrics

Number of preconditions
Number of postconditions
Lack of Cohesion in Methods (LCOM*)
Number of friend classes

Note the ratios preconditions/method and postconditions/method should tend to unity

Doc 8, Metrics part 2 Slide # 6

Metrics External at the Class level

Queries are methods that return a value
Commands are methods that don't return a value

Number of commands for k'th class, c_k
Number of queries for k'th class, q_k
Number of weighted commands for k'th class, c'_k
Number of weighted queries for k'th class, q'_k

Let Args = total number of arguments in all methods of a class
Then

c'_k = c_k + Args

q'_k = q_k+ Args

Doc 8, Metrics part 2 Slide # 7

System Level but Ignoring Relationships - Metrics

Total number of classes in system, C_s
A mean value for the number of commands per class across the system, given as:
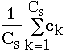
A standard deviation for c_k
A mean value for the number of queries per class across the system
A standard deviation for q_k
A mean value for the number of weighted commands per class across the system,
A standard deviation for c'_k
A mean value for the number of weighted queries per class across the system
A standard deviation for q'_k
Average class size
Standard deviation for class sizes
Distribution of class sizes
Average number of methods per class
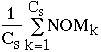
Standard deviation for NOM_k
Distribution of NOM_k
```
Doc 8, Metrics part 2 Slide # 8
```
System-Level Relationships but Excluding Inheritance
Coupling Between Objects (CBO) = fan-out

"A useful insight into the 'object-orientedness' of the design can be gained from the system wide distribution of the class fan-out values. For example a system in which a single class has very high fan-out and all other classes have low or zero fan-outs, we really have a structured, not an OO , system"

Response for a Class RFC = NLM + NRM

NLM = number of local methods in the class

NRM = number of remote methods called by methods in the class

Message-Passing Coupling (MPC)

number of send statements defined in a class

Doc 8, Metrics part 2 Slide # 9

Inheritance Coupling

Depth of Inheritance Tree (DIT) for class
Max depth of inheritance tree
Mean depth of inheritance tree
NOC_k = number of children for each class
Average NOC for the whole inheritance tree
Standard distribution of NOC for the whole inheritance tree
Distribution of NOC for the whole inheritance tree
Reuse Ratio, U
Specialization Ratio, S

where:

U = (number of superclasses)/ total number of classes

S = (number of subclasses)/ (number of superclasses)

Extreme Values of U and S

	Deep Hierarchy	Wide Hierarchy
U	1-	0
S	1+	infinity

CS 696: Advanced OO Spring Semester, 1997 Doc 8, Metrics part 2