 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Sample Sort
[To Lecture Notes Index]
San Diego State University -- This page last updated February 20, 1996, 1996

Contents of Sample Sort Lecture
Let A[1..n] be array of items,
Each item has d digits
Simple Version
for k = 1 to d do
Sort A on digit k using a stable sort
A sort is stable if two equal items retain their relative positions
Less Simple Version
Assume items have b bits
for k = 1 to b by r do
Sort A on bits k, k + 1, ..., k + r -1 using a stable sort
Stable Sort
Index[ 0 ..
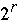 - 1] is an array of integers
- 1] is an array of integers
Seq. Counting-Rank( r, A )
for k = 0 to 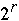 - 1
Index[ k ] = 0
for k = 1 to n do
Index[
- 1
Index[ k ] = 0
for k = 1 to n do
Index[ 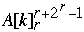 ] = Index[
] = Index[ 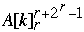 ] + 1
for k = 0 to
] + 1
for k = 0 to 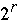 - 1 do
Index[ k ] = Index[ k -1 ] + Index[ k ]
for k = n to 1 do
B[ Index[
- 1 do
Index[ k ] = Index[ k -1 ] + Index[ k ]
for k = n to 1 do
B[ Index[ 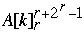 ] = A[ k ]
Index[
] = A[ k ]
Index[ 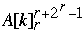 ] = Index[
] = Index[ 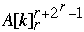 ] - 1
Where
] - 1
Where 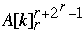 = bits r, r+1, ..., r +
= bits r, r+1, ..., r + 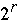 -1 of A[k]
Time Complexity
-1 of A[k]
Time Complexity
- 2*
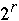 + 2*n
+ 2*n
- for Seq. Counting-Rank
-
- b/r *[2*
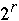 + 2*n] = O( n) for Radix sort
+ 2*n] = O( n) for Radix sort
Stable Sort - Parallelized
Each Processor gets n/p elements
Processors elements are stored in local array
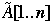
Each processor has local array Index[ 0 ..
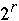 - 1] of integers
- 1] of integers
Par. Counting-Rank( r, A )
Each processor does in parallel:
for k = 0 to 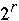 - 1
Index[ k ] = 0
for k = 1 to n/p do
Index[
- 1
Index[ k ] = 0
for k = 1 to n/p do
Index[ 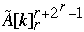 ] = Index[
] = Index[ 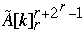 ] + 1
offset = 0
for k = 0 to
] + 1
offset = 0
for k = 0 to 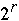 - 1 do
count = Sum( Index[ k ] )
Index[ k ] = Scan ( Index[ k ] ) + offset
offset = offset + count
for k = n/p to 1 by -1 do
B[ Index[
- 1 do
count = Sum( Index[ k ] )
Index[ k ] = Scan ( Index[ k ] ) + offset
offset = offset + count
for k = n/p to 1 by -1 do
B[ Index[ 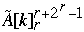 ] =
] =  Index[
Index[ 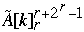 ] = Index[
] = Index[ 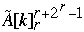 ] - 1
Time Complexity
] - 1
Time Complexity
-
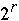 + n/p +
+ n/p +
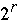 *lg(p)
+ n/p
*lg(p)
+ n/p
Parallel Radix Sort
Less Simple Version
for k = 1 to b by r do
Sort A on bits k, k + 1, ..., k + r -1 using Par. Counting-Rank
Time Complexity:
- b/r * [
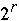 + 2n/p +
+ 2n/p +
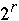 *lg(p)]
*lg(p)]
If items fit in one word than b and r are constants, so get
- C*n/p + D*lg(p), where C and D are constants
Sample Sort
n keys to sort
P processors
Each processor starts with n/P keys
Algorithm assumes keys are all distinct
If keys are not distinct, tag each key with its address
So
1 2 1 3 1 4
becomes
1, 1 2, 2 1, 3 3, 4 1, 5 4, 6
Now (a, b) < ( c, d ) if a < c or if (a = c and b < d)
Basic Idea
1 Pick P - 1 splitter keys that partition keys into P buckets
2) Send each key to proper bucket, each processor acts is a bucket
3) Keys are sorted in each bucket
Step 1 Splitters
Each processor randomly selects s ( = 32 or 64) tagged keys
All tagged keys are sorted via Radix Sort
Select tagged keys with rank s, 2s, 3s, ... , (P - 1)s to be splitters
Time Complexity:
- s for selecting s tagged keys
-
- O( n/P + lg(P) ) for sort
Note: the splitters will not partition element evenly
Some buckets will get more elements than others
Let
- L= size of the biggest bucket
-
-
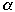 > 1
> 1
We have:
-
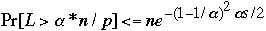
What does
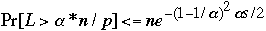 Mean?
Mean?
| n | 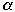 | s | 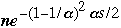 |
| 10,000 | 3 | 16 | 2.33E-01 |
| 100,000 | 3 | 16 | 2.33E+00 |
| 1,000,000 | 3 | 16 | 2.33E+01 |
| 10,000 | 3 | 32 | 5.43E-06 |
| 100,000 | 3 | 32 | 5.43E-05 |
| 1,000,000 | 3 | 32 | 5.43E-04 |
| 10,000 | 3 | 64 | 2.95E-15 |
| 100,000 | 3 | 64 | 2.95E-14 |
| 1,000,000 | 3 | 64 | 2.95E-13 |
| 10,000 | 3 | 128 | 8.71E-34 |
| 100,000 | 3 | 128 | 8.71E-33 |
| 1,000,000 | 3 | 128 | 8.71E-32 |
| 1,000,000,000,000 | 3 | 128 | 8.71E-27 |
Step 2 Send to Buckets
Node one reads each splitter
Node one broadcasts all splitters to all nodes
Each processor does binary search on splitters to determine where the proper
bucket for each key
Send each key to its bucket
Time Complexity:
- P for reading all node
-
- lg( P ) for broadcasting
-
- n/P * lg ( P ) for binary search for all keys
-
- n/ P to send keys to bucket
Step 3 Sort buckets
Use radix sort to sort buckets
Time Complexity:
- O( n/P )
Sample Sort Time Complexity
| Term | Source |
| O( n/P + lg(P) ) | (step 1 ) |
| + P + n/P * lg (P ) | (step 2 ) |
| + O( n/P ) | ( step 3 ) |
So we get O( n/P * lg( P ) + P )


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms- 1 Index[ k ] = 0 for k = 1 to n do Index[
] = Index[
] + 1 for k = 0 to
- 1 do Index[ k ] = Index[ k -1 ] + Index[ k ] for k = n to 1 do B[ Index[
] = A[ k ] Index[
] = Index[
] - 1 Where
= bits r, r+1, ..., r +
-1 of A[k] Time Complexity
- 1 Index[ k ] = 0 for k = 1 to n/p do Index[
] = Index[
] + 1 offset = 0 for k = 0 to
- 1 do count = Sum( Index[ k ] ) Index[ k ] = Scan ( Index[ k ] ) + offset offset = offset + count for k = n/p to 1 by -1 do B[ Index[
] =
Index[
] = Index[
] - 1 Time Complexity