CS 662 Theory of Parallel Algorithms
Networks
[To Lecture Notes Index]
San Diego State University -- This page last updated March 28, 1996, 1996
Static Interconnection Networks
- Processors are connected directly to other processors via point to point
communication links
Dynamic Interconnection Networks
- Processors are connected dynamically via switches
Distance
- Shortest path between two processors
Diameter
- Maximum distance between any two processors
Connectivity
- Measure of the multiplicity between two processors
Arc Connectivity
- Minimum number of communication links that can be removed to break it into
two disconnected networks
Bisection Width
- Minimum number of communication links that can be removed to break it into
two equal sized disconnected networks
Channel Width
- Number of bits that can be sent simultaneously over a communication link
- Number of wires in the communication link
Channel Rate
- Peak rate at which a single wire can deliver bits
Channel bandwidth
- Peak rate at which a communication link can deliver bits
Bisection bandwidth
- Bisection Width * Channel bandwidth
Cost
- Total number of communication links
Degree of a Processor
- Number of communication links connected to a processor
Expandability of network
- How much work is needed to add processors to an existing network
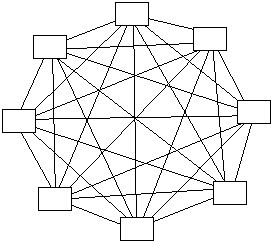
Completely-Connected network
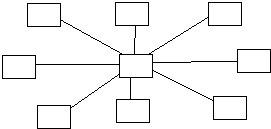
Star Network
Linear Array and Ring
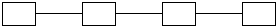
- CDC Cyperplus
Mesh Network
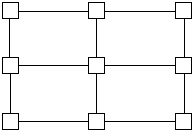
Mesh with wraparound
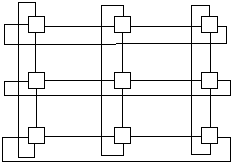
Three-dimensional Mesh
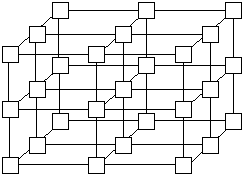
Two-Dimension Mesh Machines
- DAP, Paragon
Three-Dimension Mesh Machines
- Cray T3D, J-Machine
Tree Network
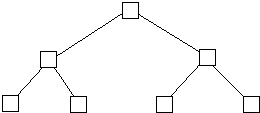
Dyanamic Tree
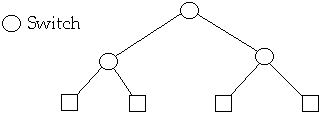
Dyanamic Fat Tree
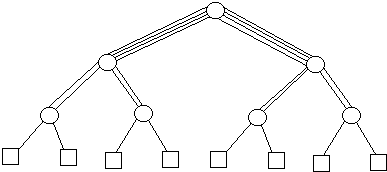
CM-5 uses a fat tree network
Hypercube
A d-dimensional hypercube consists of P =
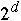processors
Recursive Definition
A zero-dimensional hypercube is a single processor
A 1-dimensional hypercube is constructed by connecting two zero-dimensional
hypercubes
A (d+1)-dimensional hypercube is constructed by connecting the corresponding
processors of two d-dimensional hypercubes
Hypercube Examples
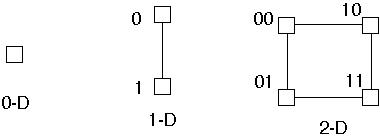
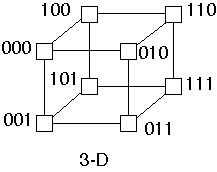
Binary Bit Definition
Label the processors 0 through
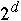in binary.
Two processors are directly connected if and only if the binary representation
of their labels differ at exactly one bit position
Hamming Distance
Let s and t be processors in a d-dimensional hypercube.
The total number of bit positions at which these labels of s and t differ is
the Hamming distance between them
The length of the shortest path between s and t is equal to the Hamming
distance between them
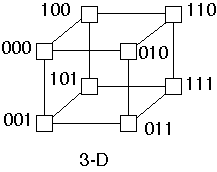
Characteristics of Networks with p Processors
| Network | Diameter | Bisection | Arc | Number of |
| | Width | Connectivity | Links |
| Completey-connected | 1 | 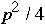 | p-1 | p(p-1)/2 |
| Star | 2 | 1 | 1 | p-1 |
| Complete binary tree | 2lg((p+1)/2) | 1 | 1 | p-1 |
| Linear array | p-1 | 1 | 1 | p-1 |
| ring | 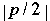 | 2 | 2 | p |
| 2-D mesh no wrap | 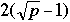 | 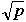 | 2 |  |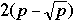
| 2-D mesh with wrap | 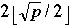 | p/2 | log p | 2p |
| Hypercube | log(p) | p/2 | log p | (plog(p))/2 |
Static
Interconnection Networks