CS 662 Theory of Parallel Algorithms
Networks part 3
[To Lecture Notes Index]
San Diego State University -- This page last updated April 18, 1996
The r-dimensional shuffle-exchange graph has:
-
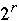nodes
-
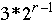edges
Label the nodes from 0 to
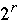-1
in binary
Two nodes U and V are connected directly by an edge if either:
- U and V differ in only in the last bit (exchange edge)
-
- U is a left or right cyclic shift of V (shuffle edge)
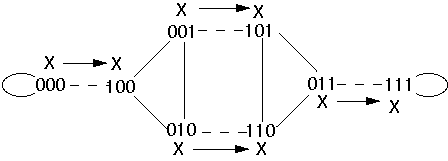
2-dimensional shuffle-exchange
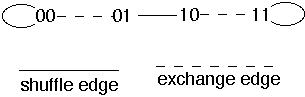3-dimensional shuffle-exchange
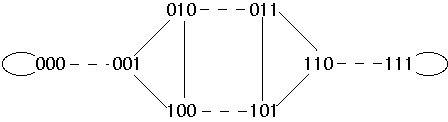
Shuffle-Exchange Simulation of Hypercube Algorithms
A normal hypercube algorithm is one in which:
-
- only one dimension of edges is used per step
-
- only consecutive dimensions are used in consecutive steps
-
- each step can consist of computation and a communication down edges of a
single dimension
Theorem
- An normal algorithm that runs in T(n) steps on an r-dimension hypercube can
be run in 2T(n) - 1 steps on an r-dimension shuffle-exchange
proof:
- Assume that the first dimension of edges used in the algorithm is K
-
- Map the process at hypercube node
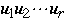to shuffle-exchange node
-
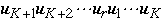
- Now processes linked by K-dimension edges in hypercube are connected by
exchange edges in shuffle-exchange
-
- So run first step of algorithm
-
- Now next step of algorithm either uses K+1 or K-1 dimension edges of
hypercube
-
- If K+1, map process stored in node
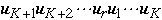to node
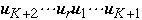by using shuffle edges.
-
- This take one step
-
- Now run the next step of algorithm
-
- If K-1, map process stored in node
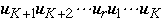to node
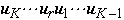by using shuffle edges in reverse direction
-
-
- Hence each "step" of the hypercube algorithm takes 2 "steps" on the
shuffle-exchange except the first step
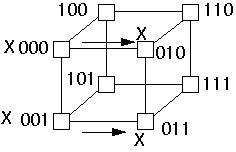
Example - Hypercube Broadcast on Shuffle-Exchange
Broadcast value from node 0
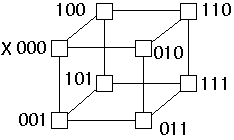
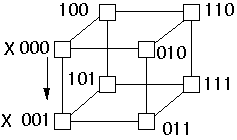
Map hypercube nodes to shuffle-exchange nodes
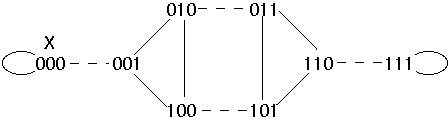
Send X down exchange edge
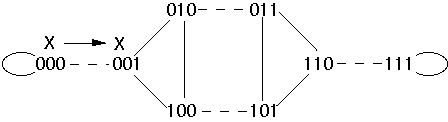Move
processes via shuffle edges
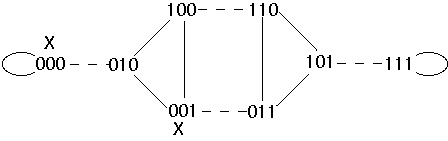
Send X down exchange edges
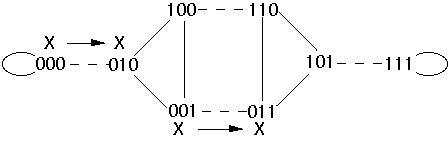
Move processes via shuffle edges
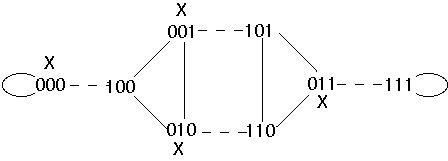
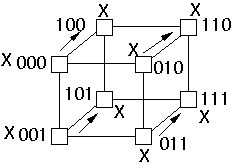
Send X down exchange edges
