CS 662 Theory of Parallel Algorithms
Chernoff Bounds
[To Lecture Notes Index]
San Diego State University -- This page last updated March 21, 1996, 1996
Bernoulli Trial
- Experiment with only two possible outcomes: success and failure
p = probability of success
q = probability of failure
q + p = 1
X(n) = number of successes during n independent Bernoulli trials
P[ event ] = the probability of event occurring
We have:
-
-
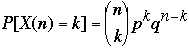
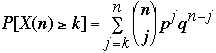
Chernoff Bounds
1)
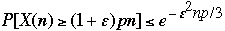
2)
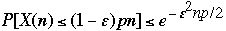
Set
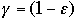and using 2) we get
3)
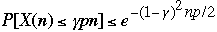
Example
What is the probability of getting 25 or fewer heads in 100 coin tosses?
p = .5
n = 100
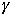= .5
-
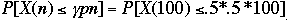
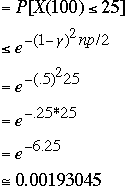
| n |  |  |  |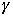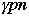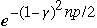
| 100 | 0.9 | 45 | 0.77880078 |
| 100 | 0.8 | 40 | 0.36787944 |
| 100 | 0.7 | 35 | 0.10539922 |
| 100 | 0.6 | 30 | 0.01831564 |
| 100 | 0.5 | 25 | 0.00193045 |
| 100 | 0.4 | 20 | 0.00012341 |
| 100 | 0.3 | 15 | 4.7851E-06 |
| 100 | 0.2 | 10 | 1.1254E-07 |
| 100 | 0.1 | 5 | 1.6052E-09 |
Randomized Algorithms
Las Vegas type algorithm
- Always generates correct answer
-
- Complexity is measured in expected value or the probability that a certain
bound will be exceeded
Monte Carlo type algorithm
- The algorithm will make errors but with a small probability
