 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Odd-Even Sort
[To Lecture Notes Index]
San Diego State University -- This page last updated February 20, 1996, 1996

Akl, The Design and Analysis of Parallel Algorithms, section 4.3
Rescheduling Principle
A parallel machine model satisfies the rescheduling principle (or slow down
principle) if given an algorithm with time complexity T on P processors and
given any s, 1 <= s <= p the algorithm can be run in s*T time using at
most
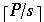 processors.
processors.
Models with uniform cost per access of shared memory satisfy the rescheduling
principle.
proof: Draw picture and wave hands
Odd-Even Transposition Sort
Assume each processor PJ contains one element xJ, for J = 1, 2, ..., N
Odd-Even Transposition Sort
- for K = 1 to
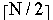 do
do
- for I = 1, 3, 5, ...,
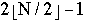 do in parallel
do in parallel
- if xI> xI+1 then swap(xI,xI+1)
- end for
- for I = 2, 4, 6, ...,
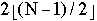 do in parallel
do in parallel
- if xI> xI+1 then swap(xI,xI+1)
- end for
- end for
A Better Odd-Even Transposition Sort
Assume we have P processors and N items to sort
Each processor has
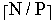 items
items
Pad the last processor with
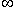 to insure it has
to insure it has
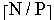 items
items
Let SJ be the items in processor PJ
Odd-Even Transposition Sort
for K = 1 to P do in parallel
QuickSort(SK)
end for
for K = 1 to 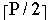 do
for I = 1, 3, 5, ...,
do
for I = 1, 3, 5, ..., 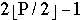 do in parallel
(s1, s2, s3, ...,
do in parallel
(s1, s2, s3, ..., 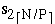 ) = sequential merge(SI, SI+1)
SI = (s1, s2, s3, ...,
) = sequential merge(SI, SI+1)
SI = (s1, s2, s3, ..., 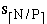 )
SI+1 = (
)
SI+1 = ( 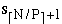 ,
, 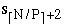 ...,
..., 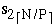 )
end for
for I = 2, 4, 6, ...,
)
end for
for I = 2, 4, 6, ..., 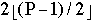 do in parallel
(s1, s2, s3, ...,
do in parallel
(s1, s2, s3, ..., 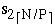 ) = sequential merge(SI, SI+1)
SI = (s1, s2, s3, ...,
) = sequential merge(SI, SI+1)
SI = (s1, s2, s3, ..., 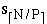 )
SI+1 = (
)
SI+1 = ( 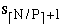 ,
, 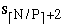 ...,
..., 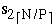 )
end for
end for
)
end for
end for


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithmsdo for I = 1, 3, 5, ...,
do in parallel (s1, s2, s3, ...,
) = sequential merge(SI, SI+1) SI = (s1, s2, s3, ...,
) SI+1 = (
,
...,
) end for for I = 2, 4, 6, ...,
do in parallel (s1, s2, s3, ...,
) = sequential merge(SI, SI+1) SI = (s1, s2, s3, ...,
) SI+1 = (
,
...,
) end for end for