CS 662: Theory of Parallel Algorithms
Final Exam 1994
[To Course Home Page]
San Diego State University -- This page last updated March 21, 1995
The following final exam was given in CS 662 offered in 1994. Not all topics covered then have been covered this year.
1. Produce the dag with minimal depth that will evaluate 3x**8 +
5x**4 + 7x**2 + 2.
2. Explain how to evaluate the polynomial y = b[1]x**(n-1) +
b[2]x**(n-2) + ... + b[n-1]x + bn for a given x using the scan
operator.
3a. Describe the odd-even transposition sort on a linear array of processors.
b. What is the time complexity and speedup of the sort if N = P. When N <
P?
4. We have N processors. Each processor flips a fair coin. Use the Chernoff
bounds to produce an upper bound on the probability that N/4 or fewer of the
processor's coin landed heads up?
5. Reduce the following to a first-order recurrence relation.
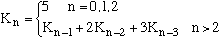
6. Explain how to compute in parallel A**-1 when A is a lower
triangular matrix. How many processors are required? How long will it
take?
7. Show how to solve for x when Ax = b using the characteristic polynomial of
a matrix.
8. Give an algorithm to compute the rank of items in a linked list. Show how
to avoid any concurrent reads or writes.
9. Explain why it is not possible to embed a complete binary tree with
2**k-1 nodes in a Hypercube with 2**k nodes.