 CS 662: Theory of Parallel Algorithms
CS 662: Theory of Parallel Algorithms
Review Questions for Final Exam 1994
[To Course Home Page]
San Diego State University -- This page last updated March 21, 1995

The following are review questions for CS 662 offered in 1994. Not all topics covered then have been covered this year.
CS 662 Spring 1994 Review topics/questions for final exam
Know the ways of classifying Parallel machines: coarse-grain, shared-memory,
message passing, SIMD, MIMD.
Measures of parallel algorithms: Speedup, cost, efficiency. Be able to compute
the measures for an algorithm. Example: An algorithm uses N*lg(N) processors
to sort N items in lg(N) time. Compute the speedup, cost, efficiency of the
algorithm.
Amdahl's law. What is the law, what does it say about parallel
algorithms? We have a parallel computer with one disk. All disk IO is done
sequentially. We have two N*N matrices on disk. We will read in the two
matrices. The two matrices will be multiplied in parallel. Independent of
what parallel algorithm we use for the multiplication, what does Amdahl's law
tell us about the possible speedup we can achieve multiplying the two matrices.
How many processors should we use for the multiplication. Is this result
reasonable.
Dags. You should be able to create a dag for a simple problem and
give the size and depth of the dag. For example, create a dag for multiplying
an N*N matrix and an N vector. What does the dag tell you about the minimum
time required for matrix-vector multiplication.
Pram model. What is the Pram model? What is the difference between
CRCW, ERCW, CREW, EREW.
What is the cost of broadcasting a datum from one processor to all processors
on an N processor CRCW (ERCW, CREW, EREW) machine?
Given an algorithm that runs in O(f(N)) steps on an CRCW machine. If we port
the algorithm to a EREW machine with the same number of processors as the CRCW
machine, what is an upper bound on the number step required by the ported
algorithm?
Rescheduling Principle. State the rescheduling principle. Given N
processors the scan operator can be performed in O(lg(N)) time. How long will
it take to perform the scan operator with N/K processors? What happens when K =
lg(N)? Give the rescheduling of the work. Can you give another example of
applying the rescheduling principle to an algorithm to make it optimal. That
is by using fewer processors the cost of the algorithm is the same as the time
complexity of the best sequential algorithm?
Scan operator.
Show how to implement quicksort with the scan operator.
Implement the +-scan operator.
Let
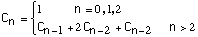
How would you compute
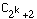 in
parallel? How many processors would you use? How long would it take?
in
parallel? How many processors would you use? How long would it take?
Sorting
Describe an O(1) sort on a CRCW machine
Describe the odd-even transposition sort on a linear array of processors.
How many comparator circuits are required in the Batchers-even odd sort to sort
a list of 2K elements.
What are the time complexity and cost of the above sorts.
Describe a parallel algorithm to find the k'th smallest item in a random list
of integers without sorting the entire list.
What is the difference between a Las Vegas and a Monty Carlo algorithm?
You are playing a game of chance. You have a six sided die (the sides are
numbered 1, 2, 3, ..., 6). You win the game if you throw the die and either a
5 or a 6 is on the top side. Give a bound on the probability of winning 10 or
fewer times in 120 games. If you pay $1.00 to play the game and get $3.00 if
you win the game. Give a bound on the probability of earning $50 or more
profit in 100 games.
What is the diameter of a N-dimensional Hypercube? a N by K mesh? a complete
binary tree with 2k-1 nodes?
Is it possible to embed a complete binary tree with 2k-1 nodes in a
2k by 2k mesh such that one edge of the tree maps to one
edge of the mesh and at most one tree node is mapped to a mesh node? Why?
Is it possible to embed a complete binary tree with 2k-1 nodes in a
Hypercube with 2k nodes? Why?
Describe an algorithm and give the time complexity and number of processors
used to:
a) evaluate a polynomial
b) multiple matrices
c) compute A-1 when A is a full matrix, when A is a lower triangular
matrix.
What is the characteristic polynomial of a matrix? How do you compute the
characteristic polynomial of a matrix? How do you use the characteristic
polynomial of a matrix to solve for x when Ax = b, where A is an N by N matrix
and b is a vector.
Graph
How do you compute the ranks of items in a linked list?
Give an algorithm to compute suffix sums of a linked list.
Write a parallel algorithm to traverse a graph and list the nodes visited in
postorder. What is the time complexity of the algorithm and how many
processors do you use?
 CS 662: Theory of Parallel Algorithms
CS 662: Theory of Parallel Algorithms CS 662: Theory of Parallel Algorithms
CS 662: Theory of Parallel Algorithms
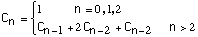
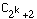 in
parallel? How many processors would you use? How long would it take?
in
parallel? How many processors would you use? How long would it take?