 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
Fall Semester, 1996
Timing Code
[To Lecture Notes Index]
San Diego State University -- This page last updated Monday, 09 September, 1996

Contents of Timing Code
- References
- Timing Analysis
- Handling Measurement Errors1
- Estimating Complexity from Timing Results
- Mathematical Analysis and Timing Code
Timing Code Slide # 1
Introduction to Mathematical Statistics, 3rd Edition, Hogg, Craig,
1970, Chapter 6
Timing Code Slide # 2
Timing in C on Rohan
main()
{
- int k, iterations;
- for (iterations = 0; iterations < 50; iterations++)
- {
- start();
- /* start the timer */
- for (k = 0; k < 2000000; k++)
- /* do some work */
- k = k;
- stop();
- /* stop the timer */
-
- printf("Time taken: %ld\n", report());
- };
}
Result on Rohan
Time Frequency Occurred
30 2
31 2
32 9
33 10
34 11
35 9
36 5
37 1
39 1
Timing Code Slide # 3
Source for Timing C Code on Rohan
#include <stdio.h>
#include <sys/times.h>
#include <limits.h>
static struct tms _start; /* Stores the starting time*/
static struct tms _stop; /* Stores the ending time*/
int start()
{
times(&_start);
}
int stop()
{
times(&_stop);
}
unsigned long report()
{
return _stop.tms_utime - _start.tms_utime;
}
main()
{
int k, iterations;
- for (iterations = 0; iterations < 50; iterations++)
- {
- start();
- /* start the timer */
-
- for (k = 0; k < 2000000; k++)
- /* do some work */
- k = k;
-
- stop();
- /* stop the timer */
-
- printf("Time taken: %ld\n", report());
- };
}
Timing Code Slide # 4
Repeat a measurement n times
Let the measurements be labeled
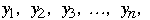
Let
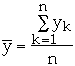 and
and
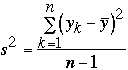
The confidence interval for the true measurement is[2]:
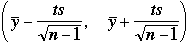
The value of t determine the probability the measurement is in the interval
When n >= 50
Probability
| 50% | 80% | 90% | 95% | 99% |
value of t
| 0.67 | 1.28 | 1.64 | 1.96 | 2.58 |
In Example
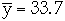 ,
s*s = 3.15, s = 1.78 selecting t = 1.96 we get
,
s*s = 3.15, s = 1.78 selecting t = 1.96 we get
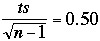
95% confidence interval is (33.20, 34.20) for actual loop time
Timing Code Slide # 5
Student t table - When n < 50
| r = n-1 | 90% | 95% | 99% |
| 1 | 6.314 | 12.706 | 63.657 |
| 2 | 2.920 | 4.303 | 9.925 |
| 3 | 2.353 | 3.182 | 5.841 |
| 4 | 2.132 | 2.776 | 4.604 |
| 5 | 2.015 | 2.571 | 4.032 |
| | |
| 6 | 1.943 | 2.447 | 3.707 |
| 7 | 1.895 | 2.365 | 3.499 |
| 8 | 1.860 | 2.306 | 3.355 |
| 9 | 1.833 | 2.262 | 3.250 |
| 10 | 1.812 | 2.228 | 3.169 |
| | |
| 20 | 1.725 | 2.086 | 2.845 |
| 30 | 1.697 | 2.042 | 2.750 |
Timing Code Slide # 6
Fun with Functions
Let f(n) = 3n*n + 4n + 5 and g(n) = 3n*n
Fact: g(n) is an approximation of f(n)
Notation: f(n) = g(n) +
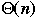
| n | f(n) | g(n) | % error |
| 1 | 12 | 3 | 75.00% |
| 10 | 345 | 300 | 13.04% |
| 20 | 1285 | 1200 | 6.61% |
| 30 | 2825 | 2700 | 4.42% |
| 40 | 4965 | 4800 | 3.32% |
| 50 | 7705 | 7500 | 2.66% |
| 60 | 11045 | 10800 | 2.22% |
| 70 | 14985 | 14700 | 1.90% |
| 80 | 19525 | 19200 | 1.66% |
| 90 | 24665 | 24300 | 1.48% |
| 100 | 30405 | 30000 | 1.33% |
| 200 | 120805 | 120000 | 0.67% |
| 300 | 271205 | 270000 | 0.44% |
Timing Code Slide # 7
Eyeballing Complexity
Let
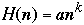 then
then
-
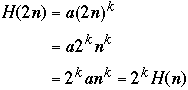
Timing Results
| N | Bubble | Insertion |
| 100 | 1 | 1 |
| 200 | 5 | 3 |
| 400 | 19 | 11 |
| 800 | 79 | 42 |
| 1600 | 317 | 166 |
Timing Code Slide # 8
Plotting Complexity
Cubic or Quadratic[3]?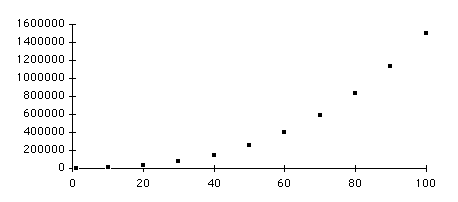
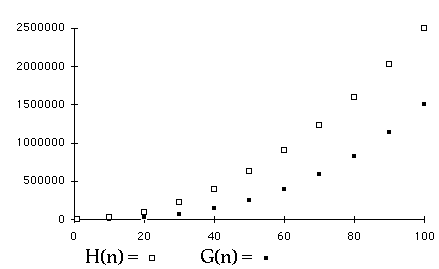
Timing Code Slide # 9
Plotting Complexity
Engineers Method (Modified)
Let
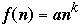 then
then
-
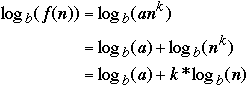
Let b = 2 and
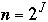 then
then
-
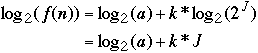
Timing Code Slide # 10
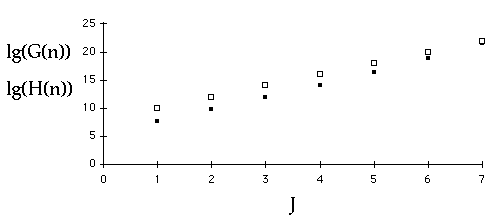
Plotting Complexity
Transform the Axis
Let
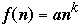 and
and
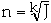 (or
(or
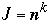 )
then:
)
then:
g(J) = f(
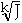 )
= a(
)
= a(
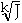 )k
= aJ
)k
= aJ
So g(J) is linear!
Timing Code Slide # 11
Example
| n | f(n) =5n*n+n + 3 | J=n*n |
| 1 | 9 | 1 |
| 10 | 513 | 100 |
| 20 | 2023 | 400 |
| 30 | 4533 | 900 |
| 40 | 8043 | 1600 |
| 50 | 12553 | 2500 |
| 60 | 18063 | 3600 |
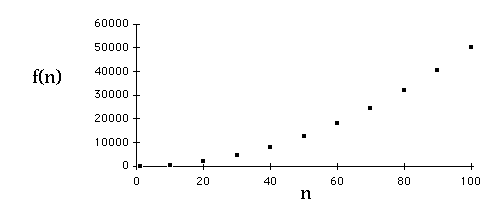
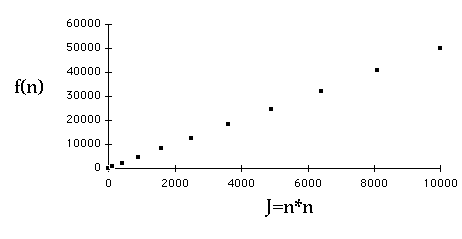
Timing Code Slide # 12
Which is Quadratic?
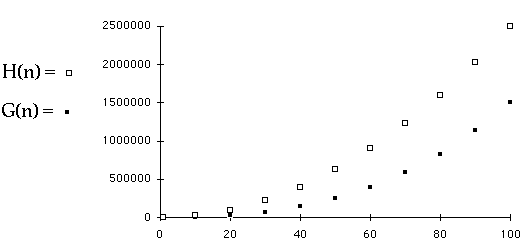
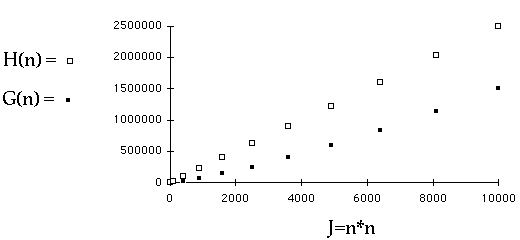
Timing Code Slide # 13
Bubble sort worst case is
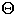 (
n*n )
(
n*n )
Complexity is an*n + bn + c
Timing Results Worst Case
| N | Bubble Sort |
| 400 | 20 |
| 500 | 31 |
| 600 | 45 |
| 700 | 61 |
| 800 | 79 |
Least Squares fit of data to an*n + bn + c
Bubble sort worst case is 0.0001143n*n + 0.01084n - 2.738
Predicted vs. Actual Time for Bubble Sort
| N | Actual | Predicted | % Error |
| 900 | 105 | 99.601 | 5.14% |
| 1000 | 124 | 122.402 | 1.29% |
| 1100 | 149 | 147.489 | 1.01% |
| 2000 | 496 | 476.142 | 4.00% |
| 2400 | 713 | 681.646 | 4.40% |
 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms