CS 660: Combinatorial Algorithms
Leda Assignment
[To Lecture Notes Index]
San Diego State University -- This page last updated October 3, 1995
CS 660 Programming Assignment - Trees and Dynamic Lists
Problems 1 & 2 Due
Oct. 12
Problems 3 & 4 Due Oct. 17
1) Write a program to time the following loop:
float why;
int k, N;
read N
start time
for (k = 0; k < N; k++)
why = sin(k);
end time
We would like to get an answer within 5% of the actual running time of the
loop. How many times must you time the loop with the same value of N to be
within 5% of the actual value with 95% confidence? What happens when you vary
N?
2) Compare the time it takes to build a binary search tree with N items in
random order with the time it takes to build a-b tree (AVL tree, BB[alpha],
binary search tree, hash table, persistent tree, red-black tree, random search
tree, skip list) with N items in random order. You to investigate the
performance of two structures. One is the binary search tree, the other is
given by the table below. Compare the average access time for the two
structures.
3) Write a program to produce a list containing the integers 1 through N
randomly distributed with Zipfian (Lotka's , 80% - 20% ) probability
distribution. Recall that the Zipfian probability distribution is given by
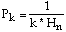for k = 1, 2, ..., n, where
.
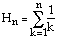Lotka's distribution is given by
.
80% - 20% distribution is given by
.
4) a) Write a program to perform move-to-front (transpose) algorithm on an
array (linked-list) of the integers 1 - N. Use the list(s) generated in 3) for
the input. Time how long the algorithm takes to find all items in the list.
See table below.
b) Write a program to produce the optimal static ordering on an array
(linked-list) of the integers 1 - N. Use the list(s) generated in 3) for the
input. Time how long it takes to search for the integers once you have the
optimal static order.
c) Time the algorithms developed in 4a & b on different files of the same
size. How do the results of the same algorithm vary between different files of
the same size and distribution. How do the different algorithms compare on the
same file?
| Name | Tree | Distribution | Algorithm | |
| Al-Shetwey | a-b tree | Zipfian | move-to-front | array |
| Barducci | AVL tree | Lotka's | move-to-front | array |
| Chen | BB[alpha] | 80% - 20% | move-to-front | array |
| Chen | binary search tree | Zipfian | transpose | array |
| Cianflone | Hash table | Lotka's | transpose | array |
| De Jaco | persistent tree | 80% - 20% | transpose | array |
| Dundon | red-black tree | Zipfian | move-to-front | linked-list |
| Floyd | random search tree | Lotka's | move-to-front | linked-list |
| Gao | skip lists | 80% - 20% | move-to-front | linked-list |
| Grab | a-b tree | Zipfian | transpose | linked-list |
| Hironaka | AVL tree | Lotka's | transpose | linked-list |
| Huss | BB[alpha] | 80% - 20% | transpose | linked-list |
| Lee | binary search tree | Zipfian | move-to-front | array |
| Leung | Hash table | Lotka's | move-to-front | array |
| Lu | persistent tree | 80% - 20% | move-to-front | array |
| Ly | red-black tree | Zipfian | transpose | array |
| Marcus | random search tree | Lotka's | transpose | array |
| Orourke | skip lists | 80% - 20% | transpose | array |
| Peker | a-b tree | Zipfian | move-to-front | linked-list |
| Pham | AVL tree | Lotka's | move-to-front | linked-list |
| Phillips | BB[alpha] | 80% - 20% | move-to-front | linked-list |
| Saunders | binary search tree | Zipfian | transpose | linked-list |
| Schmit | Hash table | Lotka's | transpose | linked-list |
| Scully | persistent tree | 80% - 20% | transpose | linked-list |
| Singer | red-black tree | Zipfian | move-to-front | array |
| Spydell | random search tree | Lotka's | move-to-front | array |
| Sun | skip lists | 80% - 20% | move-to-front | array |
| Warlop | a-b tree | Zipfian | transpose | array |
| Warrington | AVL tree | Lotka's | transpose | array |
| Williams | BB[alpha] | 80% - 20% | transpose | array |
| Wong | binary search tree | Zipfian | move-to-front | linked-list |
| Worra | Hash table | Lotka's | move-to-front | linked-list |
| Xiao | persistent tree | 80% - 20% | move-to-front | linked-list |
| Yu | red-black tree | Zipfian | transpose | linked-list |
| Yu | random search tree | Lotka's | transpose | linked-list |
| Zhang | skip lists | 80% - 20% | transpose | linked-list |